Thermal model of IGBT module on heat sink

Hello everybody. Hopefully someone could help me with my topic.

I'm creating a dynamical thermal model of an IGBT power module from ABB:
https://www05.abb.com/global/scot/scot256.nsf/veritydisplay/70bb90c34ed25dcbc1256ff50050ef85/$file/5SNA%201200E330100_5SYA1556-03May%2005.pdf

This module is mounted onto a heat sink with water cooling. Therefore the complete system contains the IGBT module and the heat sink. Also the power module consists of an IGBT and a freewheeling diode (FWD) inside. Thus the final model must comprise the IGBT, the FWD and the heat sink.

The thermal model for the IGBT and FWD could be easily derived with the aid of datasheet parameters and equivalent RC-network (called Foster network) as depicted at Fig.A:



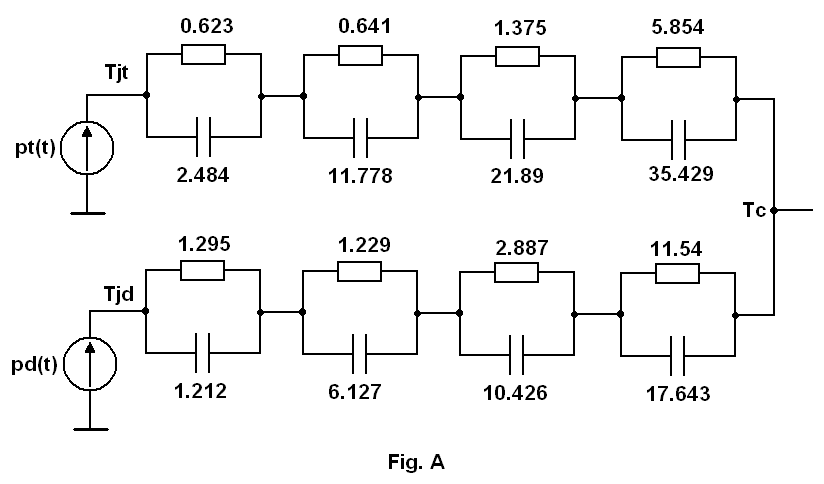
The values of capacitors and resistors are derived from the datasheet mentioned above, using the thermal impedance Zth_jc data. The terms pt(t) and pd(t) represent the instantaneous power losses in the IGBT and FWD respectively. These signals are known. Tjt and Tjd are the junction temperature of IGBT and FWD. Tc is the power module case temperature.

The case of Fig.A is well described in the literature (Seimikron Application Book, e.g.) and because of this I am pretty sure of it.

The problems start, when I'm trying to include the dynamical thermal model for the heat sink to the system. Information about this model is poor (datasheet infos are not enough, an exact description in the literature wasn't found). Thus I have done the model by myself according to the physical representaion (Cauer network) as depicted at Fig.B:



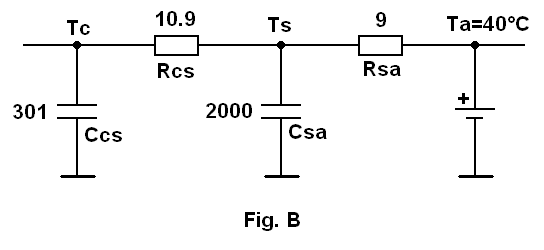
Tc - power module case temperature (the same as at Fig.A);
Ts - temperature of the heat sink;
Ta - temperature of the cooling water, which is assumed as a constant of 40 °C (modelled by a DC-source);
Ccs - thermal capacity of the power module base plate (thermal capacity of the thermal grease is neglected);
Csa - thermal capacity of the heat sink;
Rcs - thermal resistance of used thermal grease (according to its datasheet);
Rsa - thermal resistance of the heat sink provided by the manufacturer.

From this point some questions appear:

1) The MAIN QUESTION: how could the circuits at Fig.A and Fig.B be combined??? According to the literature (Semikron App.Book) it cannot be done just by connecting the circuits directly in the Tc point!

2) The thermal capacity of the base plate seems not to be included in the thermal impedance Zth_jc in the IGBT module datasheet. That's why I added it to the circuit at Fig.B as Ccs. Is it right?

3) Calculation of the thermal capacitances Ccs and Csa? I used the formula:
C = m•c, where m - mass of the material in "kg", c - specific heat of the material in "J/(kg•K)"
Is it right?

4) Is the model at Fig.B correct at all? Did I forget something?

I would be grateful for any help!

What particular value is of interest to you? The complete transient solution ... how fast the case temperature rises, or the steady state solution ... that is, how hot will the case eventually get?

If you are only interested in the steady state case temperature, Tc, then the thermal capacitances may be neglected. The inputs to the two branches would be constant, acting something like electrical DC signals.

You state that the input power signals, Pd and Pt are constant for the no heat sink case.
Could it be that the value for these two inputs will change if the heat sink is added?

Without going into the detail, I would say that connecting the devices to the heatsink @ Tc appears legitimate.
3) When you multiply m*c, dimensional analysis gives J/K, which seems correct.

user_88 said:

What particular value is of interest to you? The complete transient solution ... how fast the case temperature rises, or the steady state solution ... that is, how hot will the case eventually get?

Click to expand...

For me the complete transient solution is important. The steady state situation is clear and not interesting.

user_88 said:

You state that the input power signals, Pd and Pt are constant for the no heat sink case.
Could it be that the value for these two inputs will change if the heat sink is added?

Click to expand...

May be I didn't understand you, but the values Pt and Pd are not constants, they are the functions of time. I have these functions and can feed them into the circuit.

Two networks at Fig.A and B must be considered as one complete system. I am simply not sure, how to combine them. Therefore the situation without heat sink is not of interest for me.

The circuits at Fig.A and B cannot be joined directly in the Tc point - that follows from different papers that I read.

My humble suggestion ...

Calculate the junction branch plus heat sink ... as an independent single effort ... Laplace Transform or whatever.
Then calculate the diode branch plus heat sink .... also an independent solution.
You should at this point have a time based solution for the two components ... junction and diode.

Plot the two time solutions and find the sum of these two components ... as time progresses.

edit: ... maybe the average of the two case temperatures would be more correct ... rather than the sum.

If transistor and free-wheeling diode are integrated in the same module, a common heatsink and
case temperature may be presumed for simplification.

Click to expand...

From the Semikron handbook. I know it's not perfect but it could be good enough.

moffy said:

From the Semikron handbook. I know it's not perfect but it could be good enough.

Click to expand...

That would solve a big problem. Two power inputs into the same node is mathematically intractable.

moffy said:

If transistor and free-wheeling diode are integrated in the same module, a common heatsink and case temperature may be presumed for simplification.

Click to expand...

I've already done so. Both IGBT and FWD have the same case and heat sink temperatures Tc and Ts resp. Because of this I do not understand, how your suggestion could solve the promblem and make it possible to combine Fig.A and B? Could you please explain, what you mean.

Since you have chosen a linear model for the heatsink and power components then you can add and subtract etc. It's when you introduce non linearities into the model that this falls over. You get a first level approximation with a linear model and that is often pretty good as long as you are aware of the assumption. The quote from the Semikron handbook says that as long as both components i.e. IGBT and Diode are in the same module it is reasonable to treat their case temperature as a single entity.
Mathematically intractable, I don't doubt as heatsinks are highly non linear, but I think a practical solution is reasonable and possible.

... the earlier comment regarding an intractable solution referred to a solution method using both inputs applied to the plant at the same time.
If a superposition method .... a linear system property ...is used, then you should be able to combine two independent solutions ... one for each input branch with the heat sink branch.
... If you have another approach, please explain.

user_88 said:

... If you have another approach, please explain.

Click to expand...

Thank you all for the answers. I have some comments...

Of course, I can try to solve the problem like this:

1) Firstly I apply the powers pt(t) and pd(t) only to the circuit at Fig.A and obtain the junction temperature rise Tjt_rel(t) and Tjd_rel(t) relative to the case (assuming Tc as a constant value);

2) Then I can apply the total power losses "pt(t)+pd(t)" to the heat sink model at Fig.B and obtain the absolute case temperature Tc(t) and heat sink temperature Ts(t) dependent on the time.

3) After that the absolute juction temperaures could be obtained as a sum of relative temperaures Tjt_rel(t) and Tjd_rel(t) and the absolute temperature Tc(t):

Tjt(t) = Tjt_rel(t) + Tc(t),
Tjd(t) = Tjd_rel(t) + Tc(t).

It seem to be ok, but I have following doubts:

1) The circuit at Fig.A is specified for a constant case temperature and must be used so. Since for the Fig.B the case temperature is not constant, the results from these circuits cannot be combined (in my opinion). In other words the heat sink affects the dynamical thermal properties of the IGBT module and the circuit at the Fig.A is not directly applicable anymore.

2) If the total power losses "pt(t)+pd(t)" bypass the "junction-to-case" model at Fig.A and are fed directly to the "heat sink model" at Fig.B, the resulted case temperature Tc(t) will have excessive temperature ripples, because the pulses of the total power were not damped by the thermal capacitances of the "junction-to-case" model.

Who is this that darkeneth counsel by words without knowledge

Click to expand...

That would be me. My apologies as I have not understood the real problem, which is the model of the heatsink. Your current model assumes a constant temperature throughout, clearly not valid i.e. the cap. You would have to divide the heatsink into a number of small cubes which had minimal temperature gradient across them, and then interconnect them. Basically a 3D resistive mesh with caps representing the thermal mass of each cube at each junction. You would then have to solve this 3D matrix. You would also need elements on the surface cubes representing convection and radiation losses. Very non linear. But this wouldn't take into account the propogation velocity of phonons within the material. I seem to vaguely remember that phonons/heat can have lowish velocities depending on the material. But don't quote me on that.

This is a non trivial simulation.

moffy said:

This is a non trivial simulation.

Click to expand...

Thanks for your proposal. It's going now to turn into a real FEM simulation, what I'm striving to avoid And I'm not sure, that the FEM approach is really required here. Because if we consider the heat being spread only in one dimension (directly from case through thermal grease and heatsink to the ambient) and that the heat sink is homogeneously heated (its temperature is the same throughout the whole volume), than we can still use one RC-network for each "layer" as done at Fig.B. It would have some discrepancy from reality, but as already said, I want to avoid the FEM as long as possible.

But let me now consider another approach, that I have also found in the literature. It appears that it might be possible to convert the circuit at Fig.A to the form of the Fig.B circuit (Foster network to Cauer network). Since the Cauer network represents the physical structure of materials, it should be possible to connect the modified Fig.A to non modified Fig.B in the "Tc" point. Than the system could be modelled as a single entity. What do you think about that?

You won't get close to reality with your simplified heatsink model, especially for dynamic response. It appears that the thermal velocity of heat is relatively low, it's what they call the speed of sound for a material amongst other names. These models don't even address that, you would need delay elements to do that. And unless the heatsink is relatively small, say a water cooling block, the thermal gradients are going to be significant. It appears that it is an FEM problem. The only possible simplifications would to be use symmetry to reduce the number of dimensions of the matrix, but I can't see how that would work either.

moffy said:

You won't get close to reality with your simplified heatsink model, especially for dynamic response.

Click to expand...

I made the simulation for the steady-state and average temperature of the heatsink, and the results match the measured temperature of the heatsink very good (deviation about 1-2°C). That means, for the static case, when thermal capacitances are not considered, the model works correctly.

Unfortunately for the dynamic response I have no measurement data and cannot check my simulation results.

Ok, anyway I would like to ask one more thing, if I may. There is another one approach for junction temperature estimation, based on the experimentally obtained thermal impedance of the complete system: IGBT module + heatsink. For that the heating or cooling response of the system to a square power pulse is used. As result Zth_ja(t) is derived. Can this approach help me to avoid complex FEM simulations?