coupling and bypass capacitor value in Colpitts oscillator?

[okbro]

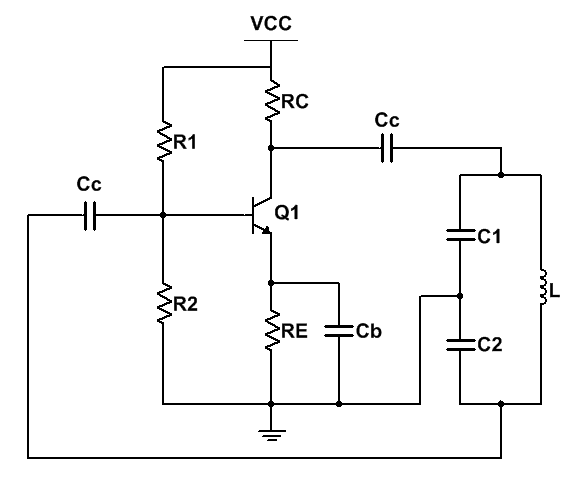
How to calculate the coupling capacitor(Cc) and bypass capacitor(Cb) value of Colpitts oscillator as shown in the diagram picture below? Suppose that the frequency of the oscillator is 5MHz, the capacitor and inductor value can be calculated but I don't know how to calculate the bypass and coupling capacitor value.

 

[Nigel Goodwin]

They don't really need to be 'calculated', as they don't need to be any specific value - they simply need to be of insignificant reactance at the frequency in question, without going stupidly large.

Anything from 1000pF to 0.1uF should be perfectly fine.

 

[JimB]

rather than re-inventing the wheel, can I refer you back to a post which I made a couple of years ago on the subject of Colpitts oscillators.

https://www.electro-tech-online.com/threads/lc-clapp-oscillator-capacitive-divider-how-to-decide-on-values.159831/

The circuit shown in that post is a bit different from your circuit, but it does work.
Please note that in your circuit you have two instances of Cc, you only need one of them for the circuit to work.

If you have any questions, please ask.

JimB

 

[danadak]

Some considerations :

Note below depends on your design goals for spectral content (if you care), T and V
goals.....so read with one eye closed

1) The bypass cap controls the amount of - fdbk generated from the emitter bias R.
That in turn affects the spectral response/purity of the waveform generated. Also
- fdbk affects oscillator startup time, additionally too much can prevent oscillation.
So one might experiment with that, eg. size of cap. I would start with a reactance of
1/10 of the emitter R at the osc frequency.

2) The coupling cap does not want to have a lot of parasitic L in it, so care here again
matters. You want most of the collector signal delivered to the tank. But there is a tradeoff,
the transistor T and V characteristics get coupled as well so too small a C and osc does not
start, too large and you affect fine T and V osc frequency and amplitude. The Tank Q I would
think would be a good staring point, eg maintain it by not over coupling the transistor
output Z, yet not too little fdbk that would compromise adequate start up of osc. Also
aggravating this is you will typically run the transistor "hot" so it has plenty of G but that
means its Zout drops, so over coupling that onto tank circuit affects stability.

Of course pay attention to type of C you use, at RF typically ceramics, micas. Critical in the actual
tuning circuit, but can affect (via their "reflected C) in coupling applications. But ceramics
in turn have T drift issues so select accordingly. There are variants of the C vs T slope used to
compensate for osc drift in many designs.

There are IEEE papers, back in the 60's and 70's, that discuss a lot of these considerations.
Don't get too brain fried on this, non linear oscillators, which this is to some extent, can soak
up your life juices essence for many years ? The Skeksis will be looking for you.....


Regards, Dana.

 

[okbro]

rather than re-inventing the wheel, can I refer you back to a post which I made a couple of years ago on the subject of Colpitts oscillators.

https://www.electro-tech-online.com/threads/lc-clapp-oscillator-capacitive-divider-how-to-decide-on-values.159831/

The circuit shown in that post is a bit different from your circuit, but it does work.
Please note that in your circuit you have two instances of Cc, you only need one of them for the circuit to work.

If you have any questions, please ask.

JimB

I read the thread you mentioned before posting my question, will read more in details, thanks

 

[danadak]

One aside, when you examine problems like this you will hear the term "reflected C" or "reflected L".

Those terms apply to the equivlenacy of a series RLC circuit to a parallel equivalent circuit.

The way to map this is

Contact Support

So if you have a series RC for example, you can calc the equivalent parallel C thru above
calculations. Gives you a feel for the affects a cap loading in a series load can have. Of course you can do
the inverse calc as well. Its all good.

These transforms often used in RF filter design and other work.


Regards, Dana.