Daniel Wood
Member
Hi guys,
I have been trying to keep on top of what I learnt at college and after many attempts, I just cant work out the currents in each resistor on the circuit shown below.
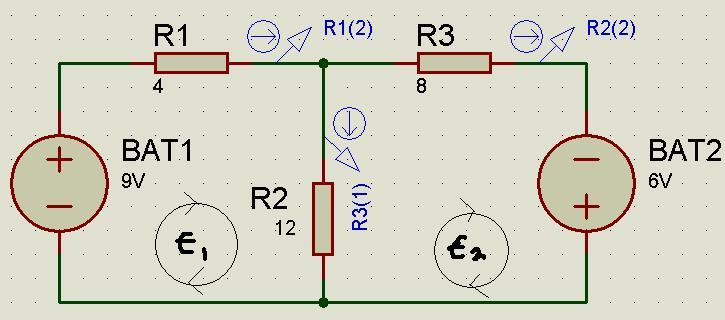
I think the confusion comes from the direction of current in each component. This ultimately leads to the calculations being different from the simulation. So anyway I assume that the current flow will be clockwise on both loops.
This is what i thought the analysis should be following the paths of E1 and E2. But we know its wrong
[LATEX]\epsilon _1 = -9 + 4_{i1} +12(i_1 - i_2) \newline \epsilon _2 = -6 + 8_{i2} +12(i_1 - i_2) [/LATEX]
After a re-arrangement we get:
[LATEX] \binom{16_{i1} - 12_{i2} = 9}{12_{i1} - 4_{i2} = 6} [/LATEX]
But we know it should be this to get the correct answers
[LATEX] \binom{16_{i1} - 12_{i2} = 9}{12_{i1} - 20_{i2} = -6} [/LATEX]
Can someone please provide some insight on how to get the correct analysis of E1 and E2 without using trial and error?
Thanks
I have been trying to keep on top of what I learnt at college and after many attempts, I just cant work out the currents in each resistor on the circuit shown below.
I think the confusion comes from the direction of current in each component. This ultimately leads to the calculations being different from the simulation. So anyway I assume that the current flow will be clockwise on both loops.
This is what i thought the analysis should be following the paths of E1 and E2. But we know its wrong
[LATEX]\epsilon _1 = -9 + 4_{i1} +12(i_1 - i_2) \newline \epsilon _2 = -6 + 8_{i2} +12(i_1 - i_2) [/LATEX]
After a re-arrangement we get:
[LATEX] \binom{16_{i1} - 12_{i2} = 9}{12_{i1} - 4_{i2} = 6} [/LATEX]
But we know it should be this to get the correct answers
[LATEX] \binom{16_{i1} - 12_{i2} = 9}{12_{i1} - 20_{i2} = -6} [/LATEX]
Can someone please provide some insight on how to get the correct analysis of E1 and E2 without using trial and error?
Thanks


