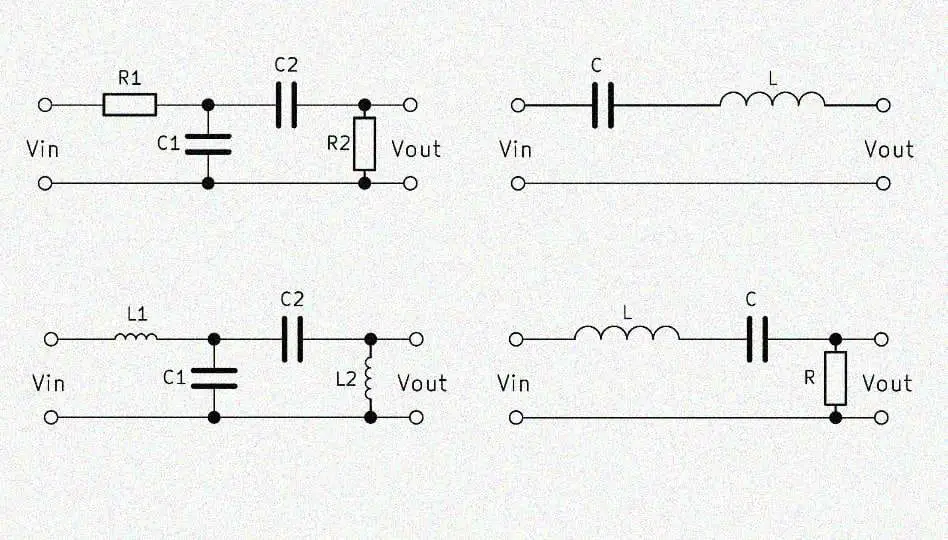
I would like to build, from passive components, a single stage variable bandpass filter for a white noise source that operates across a range of about 100Hz to 10KHz. I realize the Q will be extremely low, but this is just a starting point that I will add to.
Can someone please advise regarding a suitable circuit configuration, and how to determine RC values for a mid point of about 5KHz? Being variable, the circuit would need to incorporate a potentiometer.
The diagram from the web, attached below, is included for comment.
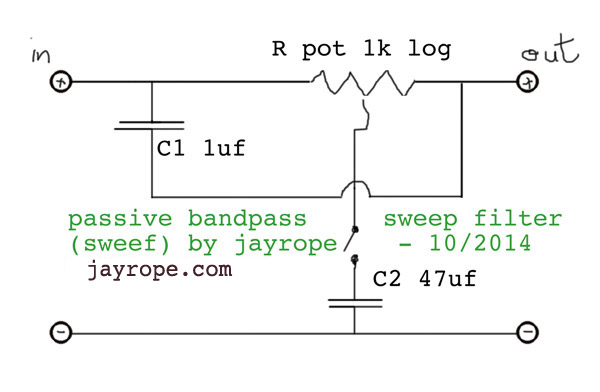
Can someone please advise regarding a suitable circuit configuration, and how to determine RC values for a mid point of about 5KHz? Being variable, the circuit would need to incorporate a potentiometer.
The diagram from the web, attached below, is included for comment.