Power dissipation from simulation circuits in LTspice?

[mading2018]

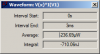
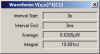
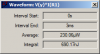
I starting a new thread now. I know how to get the power dissipation, taken the average value of the instaneous power with the thermometer probe over a component. But how come that the losses shows different each time? If I compare the circuit of an interleaved PFC and a boost PFC, where the recitfiers are exactly the same with the same input, they still give different values...why is that?

I thinking also to skip to measure the capacitors in the circuit in the simulation, cause they shows just too high values, from 100 W up to 500 W..maybe it is not accurate to measure capacitors..

 

[ronsimpson]

I thinking also to skip to measure the capacitors in the circuit in the simulation, cause they shows just too high values, from 100 W up to 500 W..maybe it is not accurate to measure capacitors..

I agree. 100W in a capacitor is wrong. If you said 0.3 watts I would agree. So this SPICE tool is not the right tool for this job.
Because you are using a "perfect" capacitor there should be zero power loss. That is my point. A perfect capacitor should have a power loss of 0 not 400 watts.
Same thing for you inductor. It is perfect so the power loss is zero. Yet your tool is saying kwatts.

 

[mading2018]

Yes, I agree but I notice now that if I run the simulation for a longer time, the power dissipation for capacitor looks much better.
After 2.5 seconds running time, I got -729.3mW.
After 1.5 seconds I got 0.641 W.
After 1 second I got 4.5414W.

So how long time should I run it? Until it is in steady state? Or should I still skip it anyway as we said.

--edit--
Oh, I saw in the other thread that you said it should be at least 100ms since the PFC take some time to running stable. But for my case, I am suppose to obtain the losses from a slow (low power) charger that is used for hours. What should I use for running time in that case?

 

[mading2018]

alec_t, ronsimpson or crutschow , do you know how long time I should run the simulation regarding to post #3 ?

 

[ronsimpson]

I think a complex PWM is not a good place to start.
We should prove our method to measure power loss in a very simple circuit.
Commonly I use Ploss=ESR*I^2 (Power loss in a capacitor = Internal Series Resistance * Current squared)

I was able to make a circuit in SPICE where the V*I was very large. By changing the DC on the cap SPICE will produce a very large positive number or a large negative number or zero. The "power loss" was zero.
----------------------
WIMA capacitor company uses "dissipation factor" to find power loss. I find that hard on my head.
Some capacitor companies use "ESR" to find power loss. Easy on my head.
Either way the power loss is related to the resistance inside the cap. It is not related to the voltage on the cap.
What I have said all week is that this "magic SPICE button" should not be used on capacitor or inductors. It is not giving you power loss. (works for resistors)

 

[mading2018]

this "magic SPICE button" should not be used on capacitor or inductors. It is not giving you power loss. (works for resistors)

Okay, I see. then I skip to measure the capacitor and inductors. I select 300ms as before.

 

[mading2018]

But that the losses are so low, is it because the average of instantaneous power is measured, which is the power losses at a specific time point (in this case after 300ms)?

 

[MikeMl]

Look at this simple circuit modeled in LTSpice. The top plot pane shows three voltages V(x), Y(y), and (V(x)-V(y)), and the current in the circuit I(R1), {same as I(C1) and -I(V1)}.

Y(y) is in phase with I(R1); you would expect lots of power to be dissipated in R1. On the other hand, look at the phase relationship between (V(x)-V(y)) and I(R1). Notice that they are in phase quadrature, so you would expect the capacitor power to be zero.



The lower plot pane shows the a plot of the Power=E*I (as found using the thermometer gimmick) of the source V1, the capacitor C1, and the resistor R1. Remember that -I(V1) = I(C1) = I(R1)! Using the CTRL-left-mouse-click on the Power waveforms gets us these three integrals:






Note that the source supplies 236.7uW, the capacitor power is 6.6uW and the resistor dissipates 230uW. So how can the capacitor take real power of 6.6uW? Note the start-up transient; it takes a bit for the waves to stabilize, during which the capacitor charges. It takes power to charge the capacitor which it might eventually give back. However, I specified the integration interval to be only three cycles, so it took 6.6uW to charge the capacitor....

LTSpice does the right thing; we just have to be smart enough to appreciate that...