Signal flow graph for two-port network

[hanhan]

Hi, this is part of an application note entitled "Low-Noise Amplifier Stability Concept to Practical Considerations" from Maxim.
Could you help me with the question in the picture? Thanks.
Source: https://www.maximintegrated.com/app-notes/index.mvp/id/1849

 

[steveB]

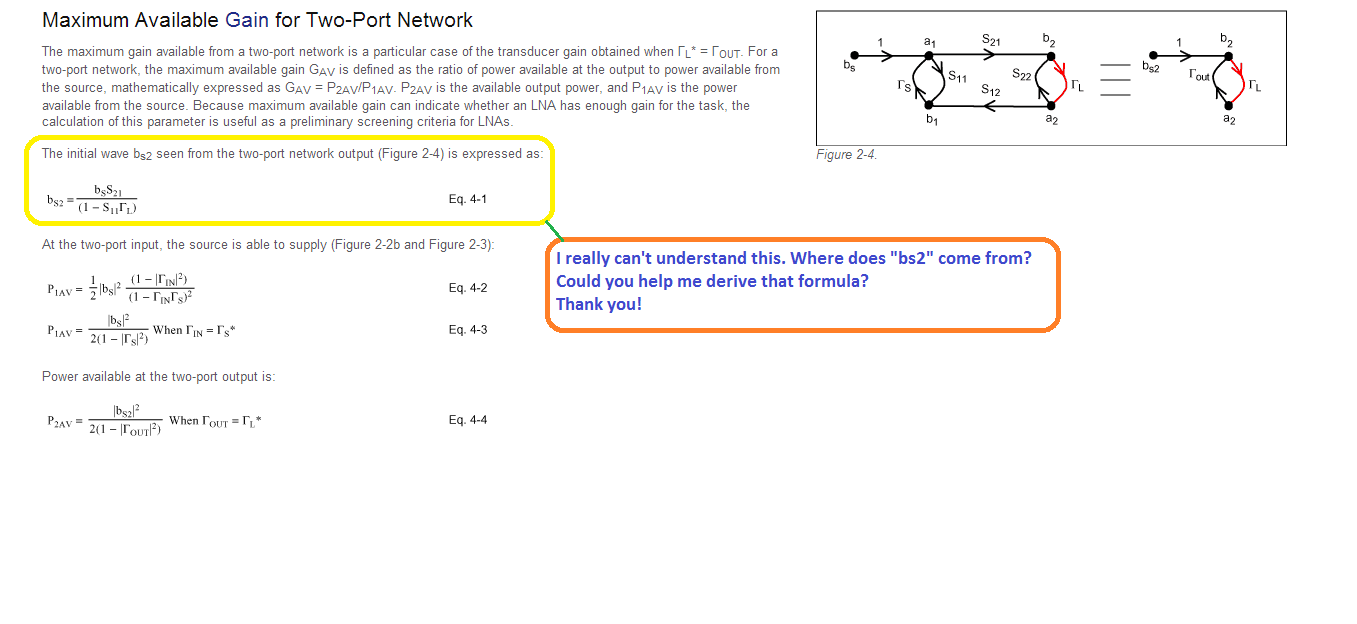
Your question is not entirely clear. Overall, bs2 comes from the analysis. The linear equations are written. Then, the signal flow graph is made from the linear equations. And, finally Mason's gain formula is applied to the flow graph to get the formula for bs2.

It's not clear from your question which parts of that are giving you trouble, although, is seems you are asking about the last step, which is the application of Mason's Gain formula. If that is your question, you need to look up and study Mason's Gain formula. Or, you can use signal flowgraph simplification rules. But, the former is easier than the latter, most likely.

EDIT: By the way, my quick look at it makes me question whether there is a typo in that formula. Please check it and see if you think it should be [latex]\Gamma_S[/latex] instead of [latex]\Gamma_L[/latex] in that formula.

 

[hanhan]

Thank you, Steve.
I studied Mason's Gain formula in Control theory course and I think I can use it here. My confusion is from the Figure 2.4. I think once I understand that, the computation is not so difficult.
What is the rule to simplify the left picture to the right one in Figure 2.4?
I can't figure out what part of the left figure is used to calculate bs2.

 

[steveB]

My thought is that bs2/bs is basically b2/bs, with the load (shown with the red arrow) removed. This is why I thought that there is a typo in that equation. But, please double check me to make sure.

You can see that the rout value is found as the transfer function b2/a2 with the load removed. I checked this formula and it looks correct. However, their formula for bs2/bs does not look correct to me.

 

[hanhan]

Thank you. The symbol bs2 was really confusing. With your suggestion, bs2 = bs and load removed, I have calculated this:

[LATEX]\frac{ b_{2} }{b_{s}} = S_{21} + S_{ 21 } \Gamma _{s}S_{11} \ast (1 + \Gamma _{s}S_{11} + (\Gamma _{s}S_{11})^{2} + ...) [/LATEX]

[LATEX]\frac{ b_{2} }{b_{s}} = S_{ 21 } + S_{ 21 } \Gamma _{s}S_{11} \frac{1}{1- \Gamma _{s}S_{11}} = \frac{S_{21}}{1- \Gamma _{s}S_{11}}[/LATEX]
You are correct. It should be [LATEX] \Gamma _{S} [/LATEX] there.
I also calculated [LATEX] \Gamma _{out} [/LATEX] before posting the thread and it is correct.
However, I still don't understand why two figures are equal then. Why we have to remove the load as calculating b2/bs?

 

[steveB]

Removing the load is just a way to make an equivalent representation. You don't have to remove the load, but it is a common method to simplify.

As to why it is equivalent, consider the following. The a2 node is independent of the bs input. So if you remove the load and make the correct transfer functions between bs and b2 and a2 and b2, then the representation is the same and you still have the needed nodes to connect the load too.

 

[hanhan]

Yeah! I see it now. Thanks.

 

[hanhan]

I want to ask another question. The load is connected between a2 and b2 and therefore, to convert the left diagram to the right one we only have to calculate b2/bs and a2/bs, right?
b2/bs can be calculated as above. However, with a2/bs, there is no direct ways to compute and we have to calculate it indirectly through b2.
a2/bs =a2/b2 * b2/bs and the only thing needed now is to find out a2/b2 or[LATEX] 1/ \Gamma _{out} [/LATEX]

In short, to find an equivalent diagram, all we need is to calculate all relations between output nodes( a2 and b2 in the example above) and source (bs in the example above).
Is that right?

 

[hanhan]

Here is another example. Assume that in that figure above, the load is connected between b1 and a2. To find the equivalent diagram, I need to find b1 or b2 in terms of bs and then find the relation between b1 and a2.
I am wondering if I understand that correctly.

 

[steveB]

I want to ask another question. The load is connected between a2 and b2 and therefore, to convert the left diagram to the right one we only have to calculate b2/bs and a2/bs, right?
b2/bs can be calculated as above. However, with a2/bs, there is no direct ways to compute and we have to calculate it indirectly through b2.
a2/bs =a2/b2 * b2/bs and the only thing needed now is to find out a2/b2 or[LATEX] 1/ \Gamma _{out} [/LATEX]

I am confused about what you are saying in this top part of what you said. I think you are saying to include the load withing this context. And, if you do, there is a direct way to compute a2/bs using Mason's gain formula. Yes, a2 depends on b2, but that is not all that important to the process. You can note that if the load is left in, then b2 also depends on a2. Essentially, once you have feedbacks, it's hard to say what depends on what.

In short, to find an equivalent diagram, all we need is to calculate all relations between output nodes( a2 and b2 in the example above) and source (bs in the example above).
Is that right?

If I'm understanding you correctly, I think I agree with this. I see no reason why this will not create an equivalent graph. However, it may not be a desirable graph in all cases because the transfer functions between the nodes will be complicated expressions. Hence, the graph does not show you anything different than the transfer function itself. One of the good things about graphs is that it lets you see the simple feedbacks and transmissions that create the complex final transfer function.

 

[steveB]

Here is another example. Assume that in that figure above, the load is connected between b1 and a2. To find the equivalent diagram, I need to find b1 or b2 in terms of bs and then find the relation between b1 and a2.
I am wondering if I understand that correctly.

First, I'm not sure there are any hard and fast rules about making equivalent diagrams/representations, in general. One is free to do anything that is mathematically correct, and provides added insight or usefulness to what you are doing.

However, with this example we can makes some observations. If the load will connect from b1 to a2, then the final equivalent diagram needs to have (at a minimum) nodes a2 and b1, and an input node that depends on bs. In this case we can see that node b2 does not matter at all, any more. This is because (with the load removed) b2 depends on the other nodes, but the other nodes do not depend on b2. Hence, if we don't care about the output b2 any more in the equivalent circuit (because the load no longer connects to it), it can be removed. Now with the load removed, a2 does not depend on any other node and the transfer function from a2 to b1 is simply S12 (i.e. it is unchanged). Then one can calculate the transfer function from bs to b1 as S11/(1 - rs S11). This will then give an equivalent diagram that you can connect the load from a2 to b1.

EDIT: I'm sorry, but I just realized I made a mistake with the above description. When I said,

" ... Now with the load removed, a2 does not depend on any other node and the transfer function from a2 to b1 is simply S12 (i.e. it is unchanged) ..."

this is incorrect. The transfer function must include the self feedback loop at the b1 node. Hence the transfer function from a2 to b1 is S12/(1 - rs S11)

 

[hanhan]

Great observations. Thank you. I am trying to make the equivalent diagram with different load nodes.

 

[hanhan]

I tried the case as load is connected between b1 and b2 shown in the picture below.

[LATEX] \Gamma _{out}= \frac{b _{2}}{b _{1}} = \Gamma _{s} S_{21} + \Gamma _{s}^{2} S_{11} S_{21} [ 1 + \Gamma _{s} S_{11} + ( \Gamma _{s} S_{11})^{2} + ...][/LATEX]
[LATEX] \Gamma _{out}= \frac{b _{2}}{b _{1}} = \Gamma _{s} S_{21} + \Gamma _{s}^{2} S_{11} S_{21}\frac{1}{1-\Gamma _{s} S_{11} } [/LATEX]
[LATEX] \Gamma _{out}= \frac{b _{2}}{b _{1}} = \frac{ \Gamma _{s} S_{21} }{1-\Gamma _{s} S_{11} }[/LATEX]

Similarly, we have:

[LATEX]\Gamma _{1}= \frac{b _{1}}{b _{s}} = \frac{ S_{11} }{1 - \Gamma _{s} S_{11} } [/LATEX]

Is that right?
Can I use the equivalent diagram in which bs and b2 are connected as follows?
( Of course [LATEX] \Gamma _{1}[/LATEX]now is a different function )

 

[steveB]

I don't seem to be getting agreement on this example. First, the original diagram has two input nodes, and the equivalent representation has removed a2, which is an input.

Still, if we zero out a2, it does not seem to agree. For example the transmission from bs to b2 should have two transmission paths and two feedback loops, and the transmission would be r1 = ( S11 + S21 rL ) / ( 1 - rs S11 - S21 rs rL ).

 

[hanhan]

First, the original diagram has two input nodes, and the equivalent representation has removed a2, which is an input.

Well, could you explain why a2 is an input node here? I always thought that there is only one input node is bs.

Still, if we zero out a2, it does not seem to agree. For example the transmission from bs to b2 should have two transmission paths and two feedback loops, and the transmission would be r1 = ( S11 + S21 rL ) / ( 1 - rs S11 - S21 rs rL ).

I think you are referring to the second equivalent in my example above as you said the transmission from bs to b2.
However, I still don't see why it has two transmission paths and two feedback loops here.
I see now that you included the rL in your calculation.
Shouldn't we remove it before calculation as previous examples?

 

[hanhan]

I think I found a great lecture here:
https://www.ittc.ku.edu/~jstiles/723/handouts/section_4_5_Signal_Flow_Graphs_lecture.pdf

 

[steveB]

Yes, that's a nice presentation.

I can quickly answer your above questions as follows.

1. In your new diagram, the a2 node is an input node because it only has arrows going out of it and no arrows going in to it. This means that it is not calculated from the other nodes and the value can only come in as an input.

2. You are correct that we should remove rL first. I misunderstood what you were trying to do. When I look at your two representations, they don't seem to match. You can double check me by applying Mason's gain formula to both cases. If you get the same answers, then you did it correctly.

 

[hanhan]

Hi,
Could you help me check if my understanding is right? Thanks.
I want to calculate b1/a2. From the picture, it seems easier to compute a2/b1.
From b1 to a2 there are two paths.
1. b1 - a1 - a2
2. b1- self loop-a2
Please check if I understood it correctly.

 

[steveB]

Hi,
Could you help me check if my understanding is right? Thanks.
I want to calculate b1/a2. From the picture, it seems easier to compute a2/b1.
From b1 to a2 there are two paths.
1. b1 - a1 - a2
2. b1- self loop-a2
Please check if I understood it correctly.

There are two issues I see with your question and understanding.

1. Neither a2, nor b1 are input nodes in your signal flow graph. Hence, you would want to modify the graph first, before calculating b1/a2 or a2/b1.
2. There is only one path. Loops are not considered paths because they come back to the same node again.

Basically, when you want to know how a variable depends on another variable, that other variable must be an input. You make it an input by removing any arrows going into it. This basically means that you remove the definition of that input variable.

It's not clear to me why y0u want to calculate b1/a2, but there is no reason why can can't do it if you choose you want to know that information.