Kerim
Member
When I heard of DDS a few years ago, I had the idea to simulate its basic configuration.
I started from a work found in the archive of LTspice group (now, at groups.io). It was done by Mr. Helmut Sennewald.
I updated his work as I see it practical for my need.
I did the version which is attached here (DirectDigitalSinewaveGenerator_DDS_v2 .zip) to see how I could build an audio sinewave generator by using DDS. Please note that most values of the generated frequencies are average ones, due to DDS frequency jitter.
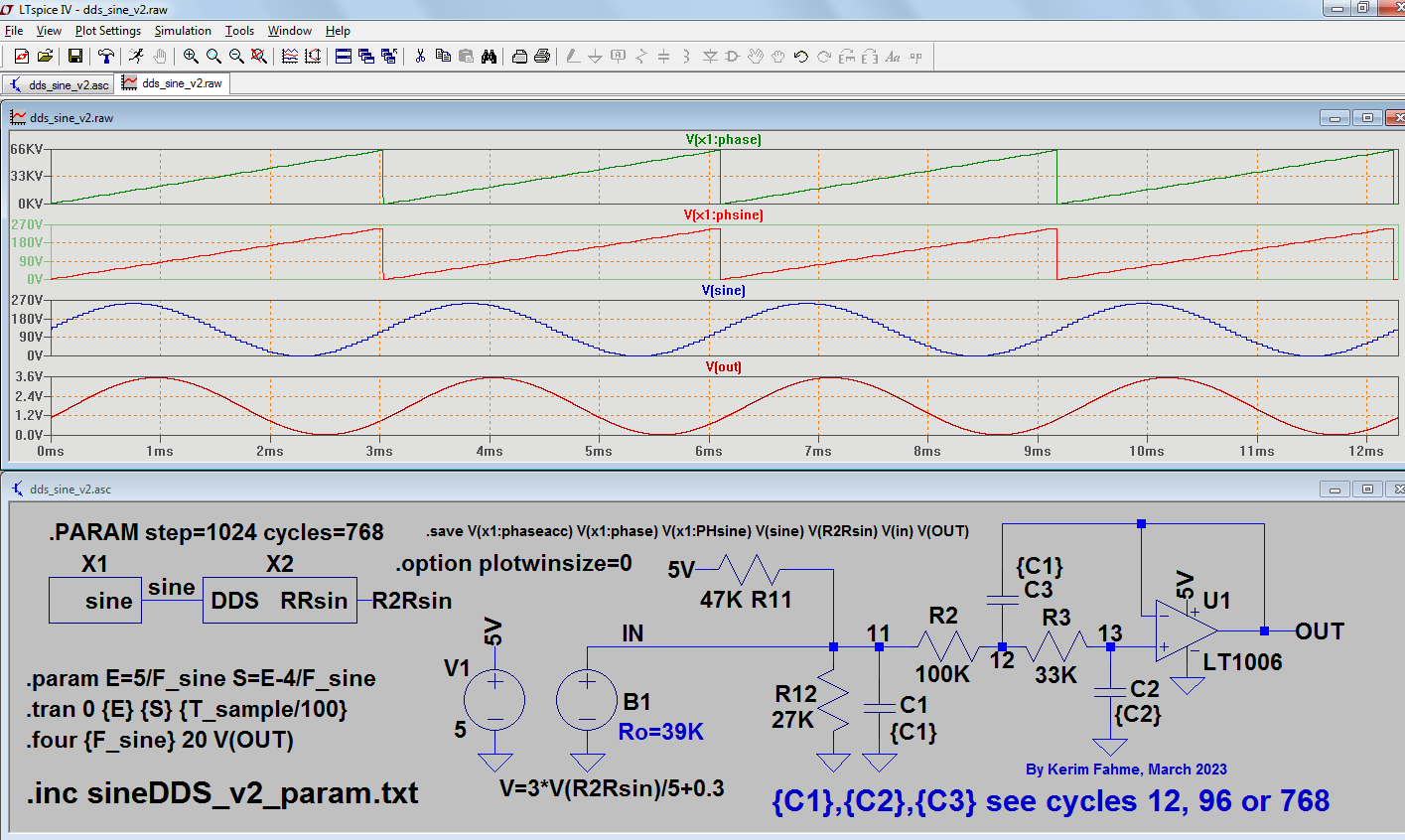
It seems that it could be done by using an 8-bit R2R ladder and a low pass filter (acts as a buffer too). The LPF here is of 3rd order, but perhaps the 2nd order is enough for the three audio bands below:
Band_1: 40.69 to 325.52 Hz, DDS loop= 768 cycles, 2^7 =< step =< 2^10
Band_2: 325.52 to 2604.17 Hz, DDS loop = 96 cycles, 2^7 =< step =< 2^10
Band_2: 2604.17 to 20833.33 Hz, DDS loop = 12 cycles, 2^7 =< step =< 2^10
Obviously, the R2R ladder is ideal in this simulation. So to implement it in real, the ladder’s resistors should be selected to have the same resistance as possible, their exact value (here, close to 39K) is not important.
Please note that the project here is for applications that are not disturbed by the frequency jitter.
Kerim
I started from a work found in the archive of LTspice group (now, at groups.io). It was done by Mr. Helmut Sennewald.
I updated his work as I see it practical for my need.
I did the version which is attached here (DirectDigitalSinewaveGenerator_DDS_v2 .zip) to see how I could build an audio sinewave generator by using DDS. Please note that most values of the generated frequencies are average ones, due to DDS frequency jitter.
It seems that it could be done by using an 8-bit R2R ladder and a low pass filter (acts as a buffer too). The LPF here is of 3rd order, but perhaps the 2nd order is enough for the three audio bands below:
Band_1: 40.69 to 325.52 Hz, DDS loop= 768 cycles, 2^7 =< step =< 2^10
Band_2: 325.52 to 2604.17 Hz, DDS loop = 96 cycles, 2^7 =< step =< 2^10
Band_2: 2604.17 to 20833.33 Hz, DDS loop = 12 cycles, 2^7 =< step =< 2^10
Obviously, the R2R ladder is ideal in this simulation. So to implement it in real, the ladder’s resistors should be selected to have the same resistance as possible, their exact value (here, close to 39K) is not important.
Please note that the project here is for applications that are not disturbed by the frequency jitter.
Kerim
| step | ACCU | F_xtl | cycles | F_sample | T_sample | F_sine |
| # | # | Hz | # | Hz | sec | Hz |
| 1024 | 65536 | 16000000 | 12 | 1333333 | 7.5E-07 | 20833.33 |
| 512 | 65536 | 16000000 | 12 | 1333333 | 7.5E-07 | 10416.67 |
| 256 | 65536 | 16000000 | 12 | 1333333 | 7.5E-07 | 5208.333 |
| 128 | 65536 | 16000000 | 12 | 1333333 | 7.5E-07 | 2604.167 |
| 1024 | 65536 | 16000000 | 96 | 166666.7 | 0.000006 | 2604.167 |
| 512 | 65536 | 16000000 | 96 | 166666.7 | 0.000006 | 1302.083 |
| 256 | 65536 | 16000000 | 96 | 166666.7 | 0.000006 | 651.0417 |
| 128 | 65536 | 16000000 | 96 | 166666.7 | 0.000006 | 325.5208 |
| 1024 | 65536 | 16000000 | 768 | 20833.33 | 0.000048 | 325.5208 |
| 512 | 65536 | 16000000 | 768 | 20833.33 | 0.000048 | 162.7604 |
| 256 | 65536 | 16000000 | 768 | 20833.33 | 0.000048 | 81.38021 |
| 128 | 65536 | 16000000 | 768 | 20833.33 | 0.000048 | 40.6901 |

