How does the feedback work in an inverting op amp amplifier?

[Heidi]

Dear friends,

The following schematic is what I draw to simulate an inverting op amp amplifier circuit.

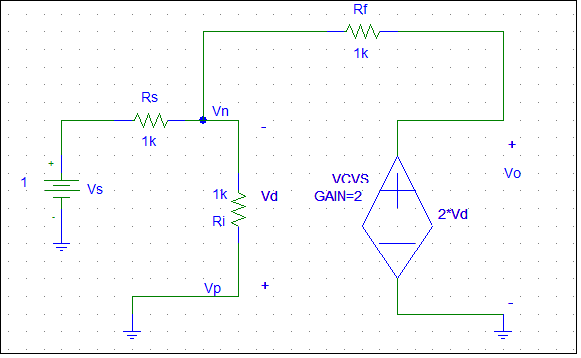
For simplicy, I make the input resistance Ri very small, neglect the output resistance, and assume that the open-loop gain equals 2.

I would like to know how the feedback works in the above circuit.

Here's what I "imagine" how it works:

First I find the difference of the input voltages, Vd=Vp-Vn.

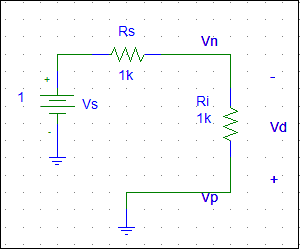
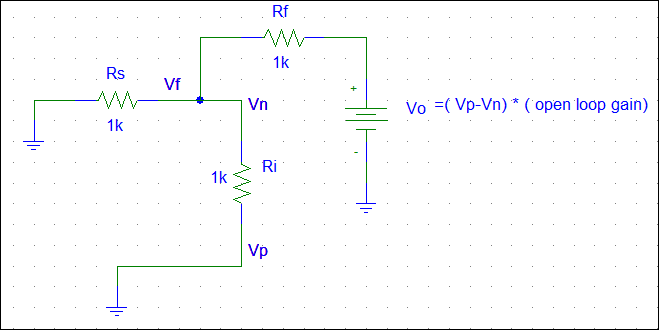
Then I assume the output voltage Vo=(open-loop gain)*Vd, and
the "feedback voltage" Vf=Vo*(0.5/(1+0.5)) by voltage dividing rule, as the following graph suggests.

Next, the new inverting input voltage Vn=(old inverting input voltage Vn) + Vf,
and the new Vd= Vp - (new Vn),
and the new Vo=(open-loop gain)*Vd,
and the new feedback voltage Vf=Vo*(0.5/(1+0.5))=Vo*1/3, ...

Starting with the voltage Vs=1V, repeating the above steps, I get the following results:

Vs=1V, Vn=500mV, Vd=Vp-Vn=0-500mV=-500mV, Vo=2*(-500mV)=-1000mV, Vf=(-1000mV)*1/3=-333.33mV

Vn=500mV-333.33mV=166.67mV, Vd=-166.67mV, Vo=2*(-166.67mV)=-333.34mV, Vf=(-333.34mV)*1/3=-111.11mV

Vn=55.56mV, Vd=-55.56mV, Vo=-111.12mV, Vf=-37.04mV

Vn=18.52mV, Vd=-18.52mV, Vo=-37.04mV, Vf=-12.35mV

Vn=6.17mV, Vd=-6.17mV, Vo=-12.34mV, ...

Obviously, if I continue iterating the same steps, the output voltage V0 will approach zero, besides, how would I know when to stop the iteration?

When I use PSpice to simulate the circuit, I get a totally different response, Vo=-400mV.

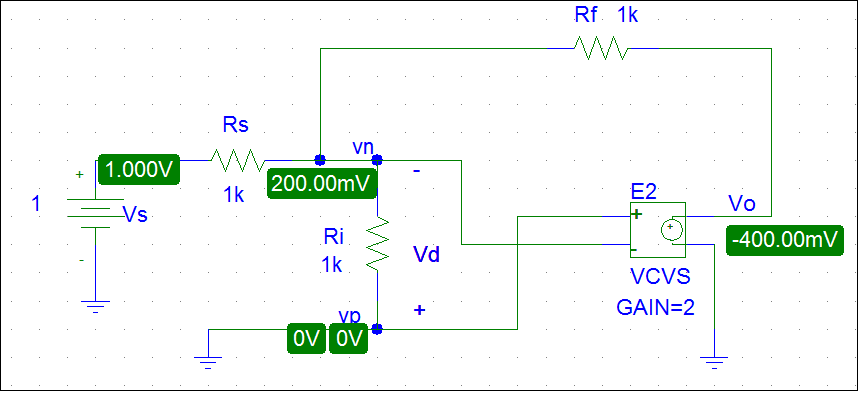
Do you know how the feedback works in that circuit? Could you explain it in a simple way?

Thank you!

 

[MikeMl]

You are on the right track, except that if the voltage-controlled voltage-source is supposed to represent an OpAmp, the open-loop-gain of the typical opamp is >200,000; not 2

Also, try it with an Ri > 10megΩ, which also better models an OpAmp

This shows what happens to the node voltages and the current through Ri as a function of the OLG (open-loop-gain) of the VCVS. The OpAmp behavior manifests itself for OLG>1K. Note that for higher values of OLG, the current through Ri approaches zero, so it serves no useful purpose, and can be removed...

 

[audioguru]

Why make a simple inverting amplifier be so complicated?
The input resistance of a modern opamp is extremely high. Its internal voltage gain is also extremely high.
Then the output voltage simply cancels the input voltage at the inverting input.
Ohm's Law can be used to show how it works like this:

 

[Heidi]

You are on the right track

Do you mean that the steps I took to evaluate the output voltage Vo is correct?

except that if the voltage-controlled voltage-source is supposed to represent an OpAmp, the open-loop-gain of the typical opamp is >200,000; not 2

OK. Let's forget about the OpAmp and its open-loop gain. Now my new question is: if I want to find the output voltage Vo of the circuit containing the voltage-controlled-voltage-source which has a gain of 2, as shown below, why would Vo approach zero at the end if I took the right steps? And the output voltage Vo was not consistent with the computer simulation result?

 

[Heidi]

Thank you, audioguru. I can find the output voltage in your OpAmp example. What I can't find is the output Vo in the following graph which has a very low input resistance Ri=1kΩ, and a very low gain 2 in the VCVS.

 

[audioguru]

Thank you, audioguru. I can find the output voltage in your OpAmp example. What I can't find is the output Vo in the following graph which has a very low input resistance Ri=1kΩ, and a very low gain 2 in the VCVS.

Then you are not talking about an opamp circuit. Your VCVS is non-inverting so with a positive input voltage and positive feedback its output will keep rising until it saturates.

 

[MikeMl]

Look at the plot I posted. I plotted your Vn (my V(inv)) and your Vo (my V(out)) for a lot of different OLGs, including 2

Reading from the plots, at OLG=2, Vn = 0.2V and Vo=-0.4V.

ps, I see what AG is talking about. In my circuit, the feedback goes to the inverting input, making the effective gain of the VCVS negative. In your circuit, the feedback is positive, so V(n) = 1V, V(o) will go to 2V, and the current in Rs is zero.

 

[Heidi]

Look at the plot I posted. I plotted your Vn (my V(inv)) and your Vo (my V(out)) for a lot of different OLGs, including 2

Reading from the plots, at OLG=2, Vn = 0.2V and Vo=-0.4V.

Oops! Yes, you're right.

The following two circuits are the same. It seems that there is nothing to do with negative feedback! Vo can be easily found to be -0.4V. I didn't draw a correct equivalent circuit for an inverting OpAmp amplifier at the first place! : )

 

[MikeMl]

I added some stuff to my previous post. Look again.

 

[Heidi]

I added some stuff to my previous post. Look again.

Thank you, MikeMl, I have seen that.

The right-hand side circuit in post #8, the voltage Vd with its positive reference polarity at ground node, the VCVS with its negative reference polarity at the ground node, hence Vd=-200mV and Vo=2*(-200)mV=-400mV.

 

[MrAl]

Oops! Yes, you're right.

The following two circuits are the same. It seems that there is nothing to do with negative feedback! Vo can be easily found to be -0.4V. I didn't draw a correct equivalent circuit for an inverting OpAmp amplifier at the first place! : )
View attachment 89844

Hi there,

A relatively simple way to do this is to just use regular circuit analysis such as nodal.

Since there are two voltage sources, we'll try using superposition to calculate vn, then go from there.
Since when we do this we end up putting two resistances in parallel and they are always 1k/2, we'll call the parallel resistance Rp to make this simpler. In real life we'd probably have two different Rp's. For this though Rp=Rs*Ri/(Ri+Rs) or Rp=Rf*Ri/(Ri+Rf)

First the response with Vin knowing the resistors set up a voltage divider:
vnA=Vin*Rp/(Rp+Rs)

Next, the response with Vo knowing the resistors also set up a voltage divider:
vnB=Vo*Rp/(Rp+Rf)

So we now have vn as the sum of these two:
vn=(Rp*Vo)/(Rp+Rf)+(Rp*Vin)/(Rs+Rp)

The next expression relates the input vn to the output Vo:
Vo=-vn*Aol

where vn is made negative because the input to the dependent source is reversed.

We have two equations now but only one unknown, Vo, so we substitute vn in for vn in the second equation and get:
Vo=Aol*(-(Rp*Vo)/(Rp+Rf)-(Rp*Vi)/(Rs+Rp))

This equation is implicit in Vo, so we solve for Vo explicitly and get:
Vo=-(Aol*Rp*(Rp+Rf)*Vi)/((Aol*Rp+Rp+Rf)*(Rs+Rp))

That is the expression that relates Vo to Vi knowing all the other parameters.

Plugging in Aol=2, Rp=1/2, Rf=1,Rs=1, we get:
Vo=-0.4*Vi

This BTW is the steady state solution. If you want to see how this works in time you'd have to have more information about the dependent source, such as it's time response.

 

[Heidi]

Since there are two voltage sources, we'll try using superposition to calculate vn, then go from there.

Thank you, MrAl.

I have no problem solving the circuit by mesh current method after noticing that a little rearrangement can be made to the original one. I thought superposition applied only when independent sources were involved. It's great to know that superposition also works here, and more importantly, I guess it provides further insight into the circuit behavior. However, I need to make sure of one thing first.

Suppose we know the value Vo=2*Vd of the dependent voltage source in Fig.2 in which only Vo is acting.

Then the voltage at node n caused by Vo acting alone can be thought of as the inverting feedback voltage. Is it correct?

This BTW is the steady state solution. If you want to see how this works in time you'd have to have more information about the dependent source, such as it's time response.

That gave me a clue as to how to modify my first imagination about how feedback works in the circuit as shown in Fig.1 above. Instead of triggering a "chain reaction" of feeding-backs on node n once the input voltage Vin is plugged in, as I described in post #1 which failed to predict the correct rsponse, I guess the VCVS is doing its feeding-back just one time, then it's over. Is it possible that things really happen this way?

It's kind of tricky to me at first. Before we can answer how much feedback is giving to node n, we have to know what the voltage Vd between ground and node n is, then we can know VCVS voltage, then we can calculate the feedback voltage, but we just don't know what Vd is going to be, how can we possibly know what the feedback will be? ... I guess it's the power of equations.

But all my inference is based on the assumption that the feedback in this case actually works as I imagined. What do you think?

Thank you!

 

[audioguru]

You need to eliminate the imaginary amplifier with a voltage gain of only 2 and use a real opamp with a voltage gain of almost one million or more.

 

[steveB]

Audioguru,

I would even recommend that Heidi take it one step further than that and consider the frequency roll-off of gain. The gain is over 1 million at DC, but it rolls off to less than two near the gain-bandwidth frequency. An infinite bandwidth op-amp is extremely "imaginary".

 

[MikeMl]

Delete this post

 

[Heidi]

Doing a purely algebraic (using Kirchoff) solution to Fig 1 in post #12, I get V0=2*Vin, which works for all values of Vin. Which means that for Fig2, V0=0.

Where is the mystery?

Hello MikeMl,

Here's how I get my answer Vo=-0.4*Vin for Vin=1V and the circuit in Fig.1.

In the left mesh: -1 + I1*1k + (I1-I2)*1k = 0
In the right mesh: (I2-I1)*1k + I2*1k + 2*Vd = 0, where Vd = (I2-I1)*1k

Simplify the two equations after substituting Vd in the 2nd equation for (I2-I1)*1k, I get
2I1 - I2 = 1 and
-3I1 + 4I2 = 0, where I1 and I2 are in mA
or
I1=(4/5) mA , I2=(3/5) mA

Vo=2*Vd=(I2 - I1)*2k = -2/5 V
for Vin=1 V, Vo =-0.4*Vin

 

[audioguru]

Audioguru,

I would even recommend that Heidi take it one step further than that and consider the frequency roll-off of gain. The gain is over 1 million at DC, but it rolls off to less than two near the gain-bandwidth frequency. An infinite bandwidth op-amp is extremely "imaginary".

Heidi's input signal is DC with no frequency.

 

[MikeMl]

For Fig1 in post #16, the algebraic solution yields Vo=-(2/5)Vin, so for Vin=1, Vo =-0.4

 

[Heidi]

You need to eliminate the imaginary amplifier with a voltage gain of only 2 and use a real opamp with a voltage gain of almost one million or more.

Hi, audioguru and steveB,

Thank you very much for your precious time. Two things I don't understand.

First I don't get why we can't analyze the circuit in Fig.1 if I only want to figure out where the feedback comes from, if any, as long as we don't treat it as an imaginary op-amp. I admit the circuit is imaginary, and it came to my mind because of op-amp, but it doesn't matter, does it?

Because the circuit only involves resistors, a DC voltage source and a dependent source, I think we don't have to consider the frequency influences for now.

For real op-amps, could you please say more about how the inverting output voltage cancels the input voltage at the inverting input and causes it to be zero Volt as the non-inverting input? I thought both input termianls are in 0 Volt because of the huge input resistance and the grounded non-inverting termianl.

EDIT: terminal, not termianl : )
EDIT: because of the huge internal input resistance of the opamp

 

[steveB]

Heidi's input signal is DC with no frequency.

The concept of DC with no frequency is even more imaginary. Nothing is constant for all time. And, the workings of feedback seem extremely mysterious until you bring time and frequency dependence into the analysis. The title of the thread is "how does feedback work?", and it seems to me that understanding the answer requires looking deeper than a DC analysis. The feedback of any real opamp circuit would not be stable in reality, but for the gain rolloff with frequency.

Anyway, I still recommend that Heidi consider not only the high gain of the opamp, but also its rolloff as frequency goes up. One of the interesting things is that since DC gain is so high, a compensated opamp must begin to start roll-off at a surprising low frequency, sometimes even below the audio range.