How is this modulating?

[JimB]

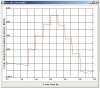
A bit of an update on the subject of resistive loading of the tuned circuit in an oscillator.

I have been doing a bit of playing around with this today and at a first pass there is a definite change in frequency as the tuned circuit is loaded.

It will be Monday before I can devote time to looking at this in detail again when I should be able to produce some meaning full measurements which I will show here on ETO.

Related to this discussion, I am sure that I remember seeing an old (transistors not invented yet) radio where the beat frequency oscillator was tuned by a variable resistor in parallel with the tuned circuit.
The radio would have been built for the British Army during the 1940s.

JimB

 

[JimB]

Today was a bit dark, wet and miserable, ideal for staying indoors and playing at electronics.

So I set up a test to run a simple oscillator and switch various resistors in parallel with the tuned circuit and measure the frequency.

The oscillator schematic and physical build is shown in the following pictures:


Not the most sophisticated circuit, but it is supposed to mimic those found as oscillators in little toy transmitters which are much spoken about on various discussion forums.
As constructed here, the oscillator runs at the lower frequency of 7.45 MHz to minimise the effect of small stray capacitance changes, compared with the effect that they would have on a similar 100MHz free running oscillator.

To switch resistors in parallel with the tuned circuit I used a four position DIP switch and four sections of a 100k SIL resistor pack.

To measure the frequency I used a Racal 1999 Counter which has a GPIB interface built in.
Using this GPIB interface I set my PC to read the frequency every second and save the value to a file.
Actually, there is a bit more to it than that, the GPIB program set the counter to display just the change in frequency from the first frequency which it measured, and then saved the change in frequency to the file.
The program to drive the GPIB interface is called EZGPIB which is freeware and was written by a German chap, Ulrich Bangert

With the data in a file, I used a program called LiveGraph (freeware, written by Greg Paperin at a university in Australia) to draw a nice graph for me.

All I had to do then was to watch the graph and flip the DIL switches, the result of which can be seen in the graph below:



As can be seen, there are four step changes in frequency as the DIP switches were closed, and four step changes as the switches were opened again.
Each switch closure added 100k Ohm in parallel with the tuned circuit.

So, the idea that the frequency of an oscillator may be changed by loading the tuned circuit with resistance seems to be supported by my experimental results.

Going all the way back to the original question "How is this modulating?" whether the modulation is caused by changes in junction capacitance in the transistor, or by loading the tuned circuit due to changes in collector resistance is still open for investigation.

If the enthusiasm remains, I may look further at the modulation process in this oscillator but that will not be until next week end as paying work will be getting in the way for the rest of this week.
Don't these people (my customers) know that I am trying to retire!

JimB

 

[davenn]

Nice work Jim

a good practical experiment with observable results

cheers
Dave

 

[EinarA]

Thank you Jim. Far too many of these threads go dead with nothing resolved or learned.
100K has a much bigger effect than I expected. Do you know the value of the inductor so I can try plugging some numbers in eqs listed in post 20. It would be better to take out the variable cap too. What is the current in the transistor?
The second eq says that Fo is affected by Hib and Hob, both properties of the transistor. Hib is Re plus Rb times ( 1-alpha); Rb is the base spreading resistance ( typically around 50 ohms ) and 1-a equals 1/ b+1. Re is .026/ Ie , so will vary with modulation. Hob is 1/ Rc and neither of my books is willing to tell me anything about how to determine its value. It seems to vary with both Ic and frequency and seems to combine both resistive and capacitive elements. I guess if it isn't given on data sheet you have to measure it yourself; not much help. In an example Osc, Hob is given as 2.66 millimhos and shifts Fo from 90 mc to 95.4. I think Fo is altered by both Rc and Ccb and little by Re.
I am definitely interested in modulation tests. DC would be most useful I think, but whatever you decide.

 

[JimB]

100K has a much bigger effect than I expected.

Me too.

Do you know the value of the inductor

About 2.2uH

It would be better to take out the variable cap too.

That is there to give a quick way of adjusting the feedback.
During these tests the plates were half meshed (about 30pF).

What is the current in the transistor?

10mA

I am definitely interested in modulation tests. DC would be most useful I think, but whatever you decide.

OK, no problem, but as I said before that will have to wait a couple of days due to work where I should be going right now, but has been delayed until tomorrow, or maybe this afternoon, or maybe ????

JimB

 

[EinarA]

Thank you for the quick response. With 390 ohms in the emitter and collector, 10 mA doesn't leave much voltage for the transistor. Perhaps you should drop it to 1 or 2 mA. What does the waveform look like. When I took some measurements on a similar low freq Osc I found the voltage was swinging way above V+, up to 35 V with a 6V supply. ( It doesn't seem pertinate, just curiousity.)

 

[JimB]

The supply decoupling resistor is actually 240 Ohm, my mistake when I sketched the circuit.

As for the voltages, have a look at this:

The channel 1 is the collector and channel 2 is the emitter.
There is not much signal at the emitter, from memory previous tests showed that the input impedance into the of the transistor is quite low, about 4 or 5 Ohms.

JimB

 

[JimB]

I am definitely interested in modulation tests. DC would be most useful I think, but whatever you decide.

I set up the oscillator as previously and connected a 100k Ohm resistor to the base of the transistor.
I then connected a variable voltage supply between the resistor and the circuit 0v line.
I set the power supply to 5v and zeroed the counter.
Varying the voltage to the base gave the results as shown by the graph below.



JimB

 

[EinarA]

Wow! A straight line. This works better as a modulator than I could have imagined. Having used it for both FM and AM it does give good sound quality. The scope trace shows less clipping than expected but much more noise. It's almost like its oscillating at two frequencies at once. Emitter impedance can be calculated from Re, 2.6 ohms at 10 mA, plus Rb divided by current gain at this freq: say 50 ohms divided by 50 for 1 ohm, plus an ohm or two for bypass ESR/L. Haven't tried to work through the other equations yet; math can be a bit of a struggle so gets put off. Placing a resistor across a tank is supposed to make the Fr go down, but your first set of data seems to show it going up. Not sure what's happening there.
According to all the books this circuit is supposed to have a cap to ground at the emitter, less than Hfe times the capacitance from collector to emitter. ( Maybe 470 pF in this case.) I wonder if adding it would clean up the waveform.
Thank you for all the great work.

 

[audioguru]

Maximum volume for a mono FM radio station is plus and minus 75kHz frequency deviation in North America but might be 50kHz in Europe then why is Jim's linear graph showing only 15kHz? It might become non-linear (distorted) with much more frequency deviation.
The oscillator is modulated by a high voltage applied to a high resistor value of 100k ohms but most audio feeds to a simple FM transmitter like this are a few hundred milli-volts through maybe 10k ohms.

 

[MrAl]

Hi,

There's no question that resistance can vary the resonant frequency of a circuit, but it depends highly on where that resistance happens to be as it is connected to the other elements. I'll illustrate below.

There is also no question that amplification (ie the transistor) can change the resonant frequency. The reason is it can change the pole locations but i wont illustrate this one here.

As a simple illustration of the first case where we have resistance that varies, consider the 'normal' parallel RLC where every element is perfect and they are all in parallel and nothing else. In this case the R does not change the resonant frequency.
However, in a parallel RLC circuit where the R is in series with the L and then the L and C are in parallel, we have the resonant frequency:
w=sqrt(sqrt(L)*sqrt(2*C*R^2+L)-C*R^2)/(sqrt(C)*L)
Note this may or may not be the same as the circuit(s) in question, but it does illustrate that a change R may be able to vary the center frequency in at least some circuits so it is not wise to adapt the blanket policy of assuming that every circuit resonance can not change with resistance.

You may want to change the form of that a little, but seeing R is inside that means it can change the resonant frequency. How much? It can easily change it by a factor of 10 to 1 depending on the choice of L and C.

Does this mean that this is the reason why the original circuit can modulate?
It's probably partly because of this and partly because of the other capacitances in the circuit. To be sure we could run a few tests. There are so many other possibilities however, such as the change in inductance with DC bias. We could in theory design a modulator that used a nonlinear inductor to change the frequency with a DC bias.

The question here however seems to be about the transistor capacitance vs the change in current alone in the transistor, which one causes the modulation. It would depend on the circuit and more importantly, the center frequency.

I like JimB's approach: test a circuit with various resistances and see what's up. We could do just that here too.

To test a given circuit, we would measure the current in the collector and then remove it entirely, replacing the collector to emitter with a single resistor. Now if the circuit can modulate with a change in resistance, changing that resistance by hand would cause a change in resonant frequency. To be able to measure this we would probably have to change the LC values to create a lower center frequency so we can measure it. We'd also have to use an external AC source to test for the resonant frequency. Unfortunately if the transistor provides amplification then we wont be able to test the effect of that.

I noticed that there have been several circuits coming up in this thread, and that the original one might not even work right. So before i did any analysis on it i'd at least want to know if the circuit works in real life or if it needs mods first.

 

[EinarA]

Trying out the equations on Jim's test circuit I get results that are opposite of what he has measured. For test 1: Fr for a parallel resonant circuit with parallel resistance is: .159* Sqrt((1/LC)-(1/4R^2C^2)). Putting in 100K for R, 2.2 uH for L, and 200 pF for C, Jim should have seen the freq shift down by 2 Hz, not up by 2KHz.
With the modulation test, I'm not completely sure the eq I have applies, but it says that Fo should increase as the bias current is increased. His really nice line goes down. I am stumped as to why.
I haven't been able to analize AG's and Al's posts yet.

 

[EinarA]

AG: Jim's circuit oscillates at 7.4 MHz, so 15 KHz of mod is equivalent to 200 KHz at 100 MHz.
Al: A parallel resistor does change the resonant frequency by the amount given in post 32. If you work through the math, you will find your equation gives the same results as mine. To my mind, I think Jim's mod test clearly shows that the change in transistor parameters is the primary factor. I just haven't been able to reconcile his results with any published equations yet. ( You can modulate just as well by feeding the signal into the emitter.)

 

[throbscottle]

There was me thinking this was going to be "well known and understood" thing! Loving the discovery process going on here!

 

[JimB]

AG wrote:

Maximum volume for a mono FM radio station is plus and minus 75kHz frequency deviation in North America but might be 50kHz in Europe then why is Jim's linear graph showing only 15kHz? It might become non-linear (distorted) with much more frequency deviation.
The oscillator is modulated by a high voltage applied to a high resistor value of 100k ohms but most audio feeds to a simple FM transmitter like this are a few hundred milli-volts through maybe 10k ohms.

As EinarA has pointed out, my oscillator is running at about 7.45MHz, the reason for this is that the test jig is a leftover from some tests which I did a couple of years ago in support of discussions about oscillators based on common base amplifier circuits.
I picked a frequency which is (about) one tenth of 100Mhz, the setting of the feedback capacitor makes a BIG difference to the frequency.
With a lower frequency, test equipment connections and hand capacitance have much less effect on circuit operation.

The reason for using a higher voltage and 100k resistance for the modulation sensitivity tests was just plain "you have to start somewhere".


EinarA wrote:

The scope trace shows less clipping than expected but much more noise. It's almost like its oscillating at two frequencies at once.

In previous tests (long ago) a vaguely remember that by minimising the collector-emitter feedback capacitance the signal became a lot cleaner.
The "noise" which you comment about is not really noise as in wideband "white" noise, but looking at the output with a spectrum analyser, there is quite an impressive "comb" of harmonics extending to well above 100MHz. I guess this is why the waveform looks a bit "wrinkly"

Thank you all for your comments, I am glad that you are enjoying the adventure.

JimB

 

[EinarA]

It is often the case that the simpler the circuit the harder it is to analyze. JimB's circuit has far too much feedback and I think this might be why the results don't match the theories. the emitter is supposed to be fed by a capacitive divider that provides just a bit more signal than needed to sustain oscillation. At 100 MHz stray capacity and low Hfe ( because you close to Ft ) mean it will work right without a cap, but I think in this case it needs one.

 

[MrAl]

AG: Jim's circuit oscillates at 7.4 MHz, so 15 KHz of mod is equivalent to 200 KHz at 100 MHz.
Al: A parallel resistor does change the resonant frequency by the amount given in post 32. If you work through the math, you will find your equation gives the same results as mine. To my mind, I think Jim's mod test clearly shows that the change in transistor parameters is the primary factor. I just haven't been able to reconcile his results with any published equations yet. ( You can modulate just as well by feeding the signal into the emitter.)

Hello,

You are not using a formula for a parallel RLC there, you are using the formula from that web site which is for a parallel RLC where some R is in series with L and some other unknown. For a pure RLC circuit, R does not change the resonant frequency. This can be observed by driving the circuit with a sine or cosine voltage source and looking at the current, or just looking at the impedance of the circuit and looking for a max or min.

Doing the latter, we end up with this equation:
(w^2*L*C-1)*(w^2*L*C+1)=0

Since either of the two factors in parens on the left above can cause a zero on the right, we choose the first one and solve that but you can see that R is already gone from the solution...
(w^2*L*C-1)=0
w^2*L*C=1
w^2=1/LC
w=sqrt(1/LC)
So we end up with a formula that includes only L and C as expected.

With the R in series with L instead, we get an entirely different solution where R can change the resonant frequency somewhat but as R gets larger the Q also goes down too so the response becomes much less sharp. It does change though and it changes enough to be able to cause frequency modulation of a 'carrier'.

I might add that the formula quoted on that linked web page does not seem to be the right formula for R in series with L and that set in parallel with C, but the author does not seem to point out the circuit he had analyzed so it is hard to say what circuit he did analyze. If someone knows this information perhaps they might mention it. But it is not for the circuit i did where R is in series with L and then those two are in parallel with C.

I also did the circuit with R1 in series with L1, R2 in series with C1 (some ESR), R3 in parallel with C (some leakage), and R4 in parallel with the other two now non ideal elements, but the formula for the resonant frequency comes out pretty long so im not sure if anyone would be interested. But this formula allows us to change any non ideality of either component to see how it affects the center frequency, as long as we use a program to do the calculations for us.

LATER:
Ok the linked to site formula was for w0 which is not necessarily the peak (or valley) frequency which is a physical artifact more than an electrical artifact. We really want to know the frequency which causes the maximum or minimum response not an intermediate quantity, so we use the frequency which causes a max or min. All of my calculations are based on this max or min because that is what appears in the circuit response when we do measurements, not w0.
However, both w0 and the real resonant peak (or valley) frequency do depend on R when R is in series with L, but for a pure RLC parallel circuit R does not change anything except the absolute value of the max or min.
This w0 is also called the 'ring' frequency, the frequency at which the network would ring at if the network was excited with a pulse. The actual peak or valley frequency however is *not* sqrt(1/LC-R^2/(4*L^2)), as there is a small difference in most cases but can be larger in other cases.
With L=1 and C=10 and R=0.5, we get for the two different formulas:
w1=sqrt(sqrt(L)*sqrt(2*C*R^2+L)-C*R^2)/(sqrt(C)*L)=0.07107
w2=sqrt(1/(C*L)-R^2/(4*L^2))=0.1936

w1 is the peak or valley formula, and w2 is the formula linked to on that other site.

 

[EinarA]

No, I did not get my formula from a web site, it is from a text book. You can change a series resistance to a parallel resistance with the formula: Rp=Rs(1+Q^2). Since we are changing the parallel resistance in this circuit, going on about series resistance is not germane. If you add series resistance to a series resonant circuit it does not change Fo. You seem to have them jumbled together. The formulas others have given are for series R in parallel resonant circuit, mine is correct for parallel R.
PS: If your eq doesn't show this effect then it is wrong.

 

[MrAl]

Hi,

To start, your equation in post #32 is ill formed. It is not clear what is in the denominator in the second term under the radical. However, assuming that all those terms multiply so they are all under the radical and since we dont need the 0.159 we get:
w3=sqrt(1/(C*L)-1/(4*C^2*R^2))

Now we have three DIFFERENT solutions:
w1=sqrt(1/(C*L)-R^2/(4*L^2))
w2=sqrt(sqrt(L)*sqrt(2*C*R^2+L)-C*R^2)/(sqrt(C)*L)
w3=sqrt(1/(C*L)-1/(4*C^2*R^2))

where
w1 is the linked site solution, w2 is my solution, w3 is your solution.

Now using L=1, C=10, R=0.4 we get three DIFFERENT numerical solutions:
w1=0.24495
w2=0.21199
w3=0.29047

and you can see that your solution does not match EITHER of the first two.

Because of this i must ask where you got this formula, and even how you can argue the point that R changes the resonant frequency in a pure element parallel circuit when you already admitted to not being sure if your formula applied in post #32.

You can not blindly apply a formula to another circuit. Converting a series circuit resistance to parallel circuit resistance does not prove anything. If you want to prove your formula is good, then prove it outright. My formula comes from a general circuit analysis of the parallel RLC circuit where there are no assumptions. It comes from a direct analysis of the impedance in the frequency domain. I did this with both circuits, the perfectly parallel one (we discuss here) and the one with series R.

w1 above has now been identified as the angular 'ring' frequency.
w2 is the angular frequency where we see the lowest point or highest point in the response.
w3 has not be identified yet, as that is your formula and you did not show where you got it from or how you got it yet.
If your formula is for a parallel RLC with no series resistance then it can not be right because it shows R in the frequency calculation when it is well known to be w=1/sqrt(LC).

Please show how you got this formula and we can go from there.

 

[EinarA]

As I said, this formula comes from an engineering text book. It says Wn equals the squareroot of (Wo squared minus alpha squared). You can find this virtually anywhere. The R in my eq is not the same as the one in yours, so you are comparing Apples and oranges. I told you how to convert them last post and if you don't know or recognize this then you don't know as much as you think you do. Wn is the angular ring frequency, straight from EE1.
Looking back at your post I see what you have done wrong. You have used the wrong alpha term: it is 1/2RC for a parallel resonance. You have used the one for series. I apologize if I sounded snippy, but you have got them jumbled.