Again your assumptions are false, and thus your conclusion is false of Caps in parallel .As I said last time, you cannot implement a single combined Cs. Therefore, the circuit does not contain any caps in series.
As we both agree
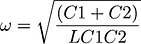
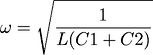
Follow along with the video below to see how to install our site as a web app on your home screen.
Note: This feature may not be available in some browsers.
Again your assumptions are false, and thus your conclusion is false of Caps in parallel .As I said last time, you cannot implement a single combined Cs. Therefore, the circuit does not contain any caps in series.
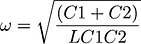
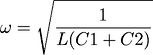
You are being seduced by the force (formula). One can write anything in a formula, but it does not necessarily mean that it is physically implementable. It is just a curious coincidence that the term for the series capacitor shows up. If there was truly a pair of series caps, then they could be combined and placed somewhere in the network. Where would they be placed? I do not say the caps are in direct parallel either.Again your assumptions are false, and thus your conclusion is false of Caps in parallel .
As we both agreeuses the series C formula rather the false formula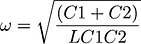 as you imply with // Caps
as you imply with // Caps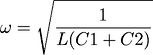
Another false claim you cannot backup which is basic 1st year stuff.Another thing, you said in post #128 that the filter network changes the phase by 180°. I believe that is wrong, and I should have caught it earlier. A passive network can only change the phase a maximum of plus or minus 90°. Since the circuit is at resonance, there is no orthogonal component to the input of the inverter. In other words, the phase change is zero from the output of the inverter back to its input during resonance. In fact, I theorize that if you connected a straight wire from the output of a inverter to its input, it would oscillate with its frequency depending on the slew rate of the inverter and other internal parameters.
Ratch
OK, I will concede that point to you. I should have run a Bode plot on it. But tell me, if a positive voltage is applied to the inverter input, the output will be a negative voltage. Then the network will change it to positive again for the input. So why doesn't the inverter lock up to its positive input value?Another false claim you cannot backup which is basic 1st year stuff.
The order of a filter can shift 90° per reactive element unless equivalent.
A passive network can shift thousands of degrees in high order filters not just 90°
Regardless of your lack of awareness, I had already showed simulation of the filter's 180° phase shift.
View attachment 96529
If I meant to build a simple LC tank circuit for AM radio tunning ( 500 kHz - 1.5 MHz), could I use this inductor??
OK, I will concede that point to you. I should have run a Bode plot on it. But tell me, if a positive voltage is applied to the inverter input, the output will be a negative voltage. Then the network will change it to positive again for the input. So why doesn't the inverter lock up to its positive input value?
Ratch
What AC loss?
There are no parasitic losses well below SRF.
The only losses with AC are the same with DC ... the DCR which was ignored.
AC core loss is significant in ferrite beads where DCR is near zero, which is a useful feature.
But AC core loss in inductors is not significant compared to ωL.
We know this since Q is high in this class of inductors.
Thus I stand by my previous comments. Try plotting Z vs f. Not L & R

