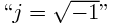PG1995
Active Member
Hi 
One of founding pillars of mathematics is that you cannot divide by zero; it's utterly absurd. Therefore, if one starts claiming that division by zero isn't absurd because it pops up while solving some problems. I think then it would cast a lot of doubt on the credibility of mathematics and give rise to disbelief in mathematics.
Another one of the founding principles of mathematics is that when you multiply any two 'real' numbers you will get a +ve number;no matter even if the numbers were -ve. Now when we write sqrt(-1), we are trying to do something which isn't allowed. I think I don't have much problem with writing swrt(-1) and calling it iota. Obviously, I would have serious problem accepting the result if it was said that sqrt(-1) equals some real number. So, I think my problem only lies in the fact that how come we end up with sqrt(-1) expression while solving other 'normal' problems. How does nature make use of such 'nonsense' expression? Could you please give me some simple example where iota is used and we can make some sense out of it? I don't think nature can make much use iota when one can't even tell which one the two or more imaginary numbers is greater; e.g. you can't tell whether 4i is greater than 2i or not! Please don't use more math to explain math. Thank you.
Regards
PG
One of founding pillars of mathematics is that you cannot divide by zero; it's utterly absurd. Therefore, if one starts claiming that division by zero isn't absurd because it pops up while solving some problems. I think then it would cast a lot of doubt on the credibility of mathematics and give rise to disbelief in mathematics.
Another one of the founding principles of mathematics is that when you multiply any two 'real' numbers you will get a +ve number;no matter even if the numbers were -ve. Now when we write sqrt(-1), we are trying to do something which isn't allowed. I think I don't have much problem with writing swrt(-1) and calling it iota. Obviously, I would have serious problem accepting the result if it was said that sqrt(-1) equals some real number. So, I think my problem only lies in the fact that how come we end up with sqrt(-1) expression while solving other 'normal' problems. How does nature make use of such 'nonsense' expression? Could you please give me some simple example where iota is used and we can make some sense out of it? I don't think nature can make much use iota when one can't even tell which one the two or more imaginary numbers is greater; e.g. you can't tell whether 4i is greater than 2i or not! Please don't use more math to explain math. Thank you.
Regards
PG