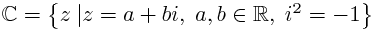All the references to Wolfram and Wikipedia assume j is a constant. The Euler reference has nothing to do with what we are talking about. None of the references show why j is a constant. They treat it like a constant and get correct answers. But we have been through that before. None of the references prove it is a constant and disprove it as being a operator. You have still not elucidated us on what jω or ωj means from a algebraic point of view.
All the references show you that
i is defined to be √-1 and it has a finite value. When i is defined to be √-1, it proves that it is not defined as an operator. Stop being stupid on purpose.
The proof in algebraic point of view is in number theory, complex numbers form a field. In history there was attempts to form complex numbers with two imaginary units, but they couldn't make it work as a number system. Then one day sir William Hamilton discovered that three dimensional complex numbers (three imaginary units, all orthogonal to each other) did work as a number system (field).. they are called "Quaternions". If j would be defined as an operator, it would work in all dimensions, but it doesn't.
https://mathworld.wolfram.com/Field.html
https://mathworld.wolfram.com/Quaternion.html
Other proof from algebraic point of view comes from the way multiplication of complex numbers is defined: (a+bi)(c+di) = (ac-bd) + (ad+bc)i
if c = 0 and d = 1, the other complex number becomes purely imaginary and unit length and the multiplication becomes: (a+bi)(0+1i) = (a0-b1) + (a1+b0)i = -b + ai
And we see that the coordinate point of the first complex number is rotated by 90 degrees. This happens because the way multiplication is defined, the value of the complex numbers and because by definition i = √-1. Not because "i is defined as rotational operator".
And here is a translation of Eulers work:
https://www.electro-tech-online.com/custompdfs/2011/09/Euler_170_Doucet.pdf
Show me some proofs and references to back up your opinions for a change. It is easy to say ignorant, meaningless, things like:
"Those are not definitions. They are symbolic representations."
"They want to call it an operator because that is what it is."
"Every signal is dynamic. If it was not dynamic, it would not be a signal."
"It is what it is regardless of how or where it is used"
"The symbol 'i' does not mean √-1. 'i' is a mathematical operator, not a finite value."