johnyradio
Member
Here's a simpler, better question.
Will these two sines experience the same percentage power loss on the same wire (passed separately, not at the same time) .
Not sure if that's equivalent to asking if they will experience the same amount of impedance.
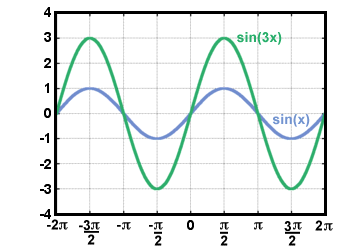
(Not homework)
Will these two sines experience the same percentage power loss on the same wire (passed separately, not at the same time) .
Not sure if that's equivalent to asking if they will experience the same amount of impedance.
(Not homework)
Last edited:

