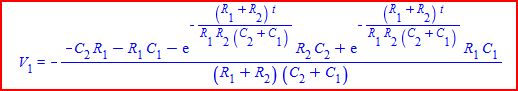How to find the time constant?

[Ratchit]

MikeML,

Whoops, second mistake you made. You did not read my post #19 where I observe that if the product of R1,C1 and R2,C2 are equal, then the time constant terms cancel out. I should have spotted it first thing myself. So that circuit contains no exponential terms even though each of the caps have a time constant. You can see it in the formula for V1 reproduced again below.

Ratch

 

[Ratchit]

steveB,

"You calculated the TC for the OPs given circuit and you obtained one value for a time constant.'

No, I obtained two equal value time constants, one for each cap.

"However, you then decided on your own to say this means there is two values, one for each capacitor. This decision is not based on any standard practice or established convention and does not make sense in a mathematical analysis, as I showed"

You made this statement before. I say again, the expression for V1 shows two different multipliers for each exponent term even though their TCs are equal.

"In the simpler case with Rs=0, There is only one state variable. It is a property of state space systems that all variables can be related back to state variables and input variables. Any variable that depends on the state variable will show the time constant value in its response. If you choose V1 as the state variable, then V2 will just be another variable that depends on V1 and it will show the same time constant. And vice versa, if you choose V2 as the state variable. You could also define a new state that is a linear combination of V1 and V2."

This circuit is symmetrical, so I expect V1 and V2 to have a relationship to each other.

"I showed the more general case with nonzero Rs. Here V1 and V2 respond with 2 time constants. Both state variables show both time constants because I didn't choose the natural state variables that would diagonalize the A matrix. When you do diagonalize the A matrix, each state variable would only show one time constant, and any other system variable that depends on both state variables would show both time constants in the response. In this example V1 and V2 will always be mixed modes that show both time constants"

That went over my head. I calculated V1 with Laplace transforms and saw two TCs.

"Time constants are always traceable back to poles (assuming the poles are on the real axis). Knowing the number of poles is important because it shows the order of a system. It's important to not say that a first order system (such as the OPs example) has 2 time constants because this will trick people into thinking it's a second order system. The more general circuit is a second order system, so there we do want to say there are two time constants, but those are not equal values, even in the case of perfect symmetry with both capacitors equal and both resistors equal."

I don't doubt that TCs and poles are related to each other. I will stick to my Laplace derivation.

Ratch

 

[MrAl]

Hello again,

You cant really go by the 'paper' linked to in order to understand this. That's because the paper is taking the most simplistic view that we can possibly take. With a series resistance Rs there can easily be three time constants that we might want to consider, and two that show up clearly in the time response.

Let me try to make this more clear...

With Rs less than the other two resistors, we see a rise in current (or voltage at the junction of R1 and R2) that is exponential and is mostly dependent on Rs and C1 and C2. That brings the response up exponentially. Then, if there is any imbalance in the ratio of R1 and R2 compared to C1 and C2 (the time response is not a constant) then we'll see the second time response kick in, where the voltage at the junction of R1 and R2 either drifts up or down with time exponentially.

But the point i was making was that in this 'second' time response period we might consider R1*C1 one time constant and R2*C2 another time constant so that we might understand the circuit in a different light. The result does not lead to an exact analysis of the response but does help sometimes. We might also look at R1*C and R2*C where C is the sum of the two capacitances, which leads to a better approximation when we hope to eliminate one set for simplicity.

 

[Heidi]

Hello, MikeMl, MrAl, Ratch, steveB, and The Electrician, I appreciate all your help, but I haven't finished my elementary circuits course, I can not understand most of the discussion you've posted here. I was thinking that I would go back to this problem later when I finish stduying Laplace transform, but 'never put until tomorrow what you can do today', I think I should say clearly what I really don't understand and hopefully get the answers, otherwise, I'd feel guilty at wasting your time.

First, please allow me to start with a new, simpler problem which is in the same ducument at https://faculty.kfupm.edu.sa/EE/husseina/081/STC_Bode_Plot.pdf

My first question is about Thevenin's theory and the voltage source. If Vs in Figure 7 is a step voltage function, and I want to find the equivalent circuit seen from the capacitor into the circuit, does Thevenin's theory still apply? The reason why I ask so is that I only have experience of finding Thevenin equivalent circuits when the sources in circuits are DC or sinusoidal functions.

Secondly, I have to ask, why do we need to know about the Thevenin's equivalent circuit of original circuit? Is the purpose to try to find the capacitor voltage function of time?

 

[The Electrician]

Yes, series/parallel resistors/caps can be combined if the resistors have the same currents and the caps are supplied with the same voltage. But, that is not the case in this circuit.

Ratch

For this circuit, if the voltage source is replaced with a short, the capacitors are then in parallel (supplied with the same voltage). This is the same situation that occurs if the source supplies some non-zero voltage for a while and then goes to zero. If the source is ideal, with zero internal resistance, the source supplying zero volts is completely equivalent to a short. The caps are then in parallel. How can there be more than one time constant then?

But if the source is supplying a non-zero voltage after a step, does that then increase the number of time constants? Looking at my scope captures, I don't see any difference in the transient waveforms other than polarity for a step from zero to a non-zero voltage, compared to a step from the non-zero voltage to zero volts.

 

[steveB]

I will stick to my Laplace derivation.

I was never in doubt of that. My purpose here is related to my hope that Heidi will not follow your lead in the future. You often seem to want to teach your own ideas even when they are contrary to accepted ways. The Laplace approach and the modern state space approach are not contradictory and yield the same information about the order of a system. Crunching a formula and seeing two exponentials with the same time constant is not an indication of a higher order system. The given circuit (despite its unrealizable form) is a first order system. Hence, one degree of freedom can only allow one pole and one time constant. By contradicting this, you just confuse the situation by telling the OP that the reference used is wrong (because it gives an example #4 as a Single Time Constant Circuit). Yet, this terminology is in perfect agreement with accepted terminology and analysis methods, while your description is not. So stick to your own ways if you want, but I see no usefulness in you teaching your own ways and contradicting standard practice.

Time constants are not often even used once the system order is greater than one anyway, because then you are likely to have complex valued poles (a system with one pole must have a real valued pole). Almost always, higher order systems are described in terms of poles and zeros. But, if a system has real valued poles, one can call them time constants, but the number of time constants equals the number of real valued poles when you do that.

Anyway, you are free to use your own methods and free to teach your own methods. But, of course I'm free to state that I don't agree with this particular interpretation you made about the method you used here.

 

[MrAl]

Time constants are not often even used once the system order is greater than one anyway, because then you are likely to have complex valued poles (a system with one pole must have a real valued pole). Almost always, higher order systems are described in terms of poles and zeros. But, if a system has real valued poles, one can call them time constants, but the number of time constants equals the number of real valued poles when you do that.

Hello there Steve,

That just doesnt sound right at all. Individual time constants are often considered in higher order systems. That's how you can tell if one is going to decay much faster than the other, which is an indication of stiffness for example.
Other systems can actually be computed based on the individual time constants and the result is the complete solution.

I think you are looking at this circuit closely and trying to generalize over all areas of circuit analysis based on this one circuit alone. It has to tbe the other way around...look at many other circuits and then look at this one and then generalize. When we do that we still see different ways of looking at it.

The new circuit doesnt contradict any physical laws so we should probably turn our attention to that one now.

 

[Ratchit]

For this circuit, if the voltage source is replaced with a short, the capacitors are then in parallel (supplied with the same voltage). This is the same situation that occurs if the source supplies some non-zero voltage for a while and then goes to zero. If the source is ideal, with zero internal resistance, the source supplying zero volts is completely equivalent to a short. The caps are then in parallel. How can there be more than one time constant then?

But if the source is supplying a non-zero voltage after a step, does that then increase the number of time constants? Looking at my scope captures, I don't see any difference in the transient waveforms other than polarity for a step from zero to a non-zero voltage, compared to a step from the non-zero voltage to zero volts.

The TCs are the same whether the caps are being energized or de-energized, so I am not surprised you observe the same transient waveforms. I addressed this question in post #29 where I calculated the voltage curve with the source voltage turned off and the caps having different initial voltages across each of them. The TCs are determined by circuit values, not by the voltage.

Ratch

 

[steveB]

Hello there Steve,

That just doesnt sound right at all. Individual time constants are often considered in higher order systems. That's how you can tell if one is going to decay much faster than the other, which is an indication of stiffness for example.
Other systems can actually be computed based on the individual time constants and the result is the complete solution.

I think you are looking at this circuit closely and trying to generalize over all areas of circuit analysis based on this one circuit alone. It has to tbe the other way around...look at many other circuits and then look at this one and then generalize. When we do that we still see different ways of looking at it.

The new circuit doesnt contradict any physical laws so we should probably turn our attention to that one now.

Hi Mr Al,

Yes, you are correct here. I didn't word what I was trying to say very well. What I'm trying to say is that higher order systems ( I typically deal with, and do control analysis on, systems with order >13) are often too complex to consider simple time constants alone. But certainly, many higher order systems can be characterized and understood from the point of view of time constants. I did exactly this when I gave the state space system and free response for that second order system with nonzero source resistance Rs. There, the two time constants fully characterize the dynamics of the system and all variables will show those two decay rates.

Just to reiterate the details of the free response, when R1=R2=R and C1=C2=C.

V1(t)=(V1(0)+V2(0)) exp(-t/T2) / 2 + (V1(0)-V2(0)) exp(-t/T1) / 2
V2(t)=(V1(0)+V2(0)) exp(-t/T2) / 2 - (V1(0)-V2(0)) exp(-t/T1) / 2

where the two time constants are T1=R C and T2=R C Rs /(2R+Rs)
and V1(0) and V2(0) are the initial capacitor voltages

Even in systems where the poles are complex, the real part of the pole says something about the decay rate of oscillatory responses, and can be interesting to consider.

 

[MikeMl]

MikeML,

Whoops, second mistake you made.

No mistake; the only mistake being made (as usual) is all of the mental masturbation that this thread has degenerated into, which is way over the OP's head!

I was trying to make this specific point:

If the OP can take this away from all of the blather, the practical utilization of the circuit being discussed is for compensation of an attenuator like a 10X O'scope probe. To cancel out any RC time constant droop or peaking, the two respective time-constants must be equal. If they are, there is no sign of the single resultant effective time-constant that I showed in post 4 and 5 of this thread.

 

[steveB]

MikeMl,

I think you made some good points in this thread.

I was trying to interpret your simulation results, but I was not sure I understood it fully, which is why I could not comment on it.
Perhaps you can explain some things that are confusing me.

1. You show V1 starting at a value of 0.5 V, but the Va and Vb start at zero, and stay that way while the V1 is steady at 0.5V. Hence, it seems that KVL is not obeyed here. Shouldn't Va=V1?

2. You mention that the current from V1 is finite, but it's not clear why. Did you somehow limit it? It seems that the mismatch in V1 with the sum of the cap voltages would cause an infinite current. And, when the voltages are matched, a perfect pulse change should induce infinite current.

I expect I'm just misunderstanding either the setup of the simulation, or not interpreting the signals correctly, and I hope you can clarify for me.

Thanks

EDIT: Sorry. So I went back to recheck the simulation you showed, and I see one cause of my confusion. I was reading your I(V1) as the V1 voltage input. My eyes are getting so bad and it looked like (V1) to me.

So, I think I understand the simulation now. A little later I'll post a comment on that.

Thanks agian

 

[Ratchit]

MikeML,

"If the OP can take this away from all of the blather, the practical utilization of the circuit being discussed is for compensation of an attenuator like a 10X O'scope probe. To cancel out any RC time constant droop or peaking, the two respective time-constants must be equal. If they are, there is no sign of the single resultant effective time-constant that I showed in post 4 and 5 of this thread. "

No need to belabor that point. In post #19, I acknowledged that when R1*C1 = R2*C2, the two TCs cancel out leaving leaving only the two R's to determine the voltage across the caps. That can be seen from the equation for V1.

Ratch

 

[MikeMl]

MikeMl,
...
Perhaps you can explain some things that are confusing me.

1. You show V1 starting at a value of 0.5 V, but the Va and Vb start at zero, and stay that way while the V1 is steady at 0.5V. Hence, it seems that KVL is not obeyed here. Shouldn't Va=V1?

In Post #4, V(a) is an example of the response of the OP's original circuit with purposely mismatched time-constants. The response shows a "combined" time-constant per the OP's attachment.
In Post#4, V(b) shows that circuit B (from the OP's attachment) has a very different behaviour than circuit A; therefore cannot be a "Thevinin Equivalent" of circuit A. By implication, it is not possible to come up with one that contains a single voltage source, one resistor, and one capacitor.
In Post#5, Circuit A and V(a) is repeated.
In Post#5, I present an "Equivalent" circuit (C), which consists of a stepped voltage source with a partial "Thevinin-like" equivalent sitting on top of it. The response V(c) is identical to V(a). The combined time-constant is per the OP's attachment.

2. You mention that the current from V1 is finite, but it's not clear why. Did you somehow limit it? It seems that the mismatch in V1 with the sum of the cap voltages would cause an infinite current. And, when the voltages are matched, a perfect pulse change should induce infinite current.

Note that in all the simulations of Posts #4, 5, 36 and 39, I am limiting the rise-time of the input voltage source. Because of the capacitive load, limiting the rise-time means that the source is only delivering a finite current to initially charge the capacitor(s). It is not necessary to limit current by adding source impedance. Only if the the rise-time of the voltage source is zero would an infinite current be required...

This is the reason a 10X scope probe is used when displaying high-speed logic signals. The effective input capacitance of a 10X scope probe is one-tenth of the scope input amplifier capacitance shunted by the cable capacitance...

 

[The Electrician]

The TCs are the same whether the caps are being energized or de-energized, so I am not surprised you observe the same transient waveforms. I addressed this question in post #29 where I calculated the voltage curve with the source voltage turned off and the caps having different initial voltages across each of them. The TCs are determined by circuit values, not by the voltage.

Ratch

If there is a short in place of the voltage source, how can there be different initial voltages across the capacitors? In that case the two capacitors are connected in parallel.

 

[MikeMl]

...
First, please allow me to start with a new, simpler problem which is in the same ducument at https://faculty.kfupm.edu.sa/EE/husseina/081/STC_Bode_Plot.pdf

My first question is about Thevenin's theory and the voltage source. If Vs in Figure 7 is a step voltage function, and I want to find the equivalent circuit seen from the capacitor into the circuit, does Thevenin's theory still apply?...

Secondly, I have to ask, why do we need to know about the Thevenin's equivalent circuit of original circuit? Is the purpose to try to find the capacitor voltage function of time?

Here is simulation which illustrates your question about a stepped voltage source. I show that the response of the original V(a) and Thevenin Equivalent circuit V(b) are identical. Note that only the amplitude of the stepped source needs to be modified from 3V to 2V to create the Thevenin equivalent source; all of the timing parameters remain the same...

btw: LTSpice's pulsed voltage source has the following parameters:

PULSE(V1 V2 Tdelay Trise Tfall Ton ...)

 

[steveB]

MikeMl,

Thanks for explaining. Actually the cause of my confusion was in post #39 where i was reading the current waveform I(V1) as if it was the input voltage. It's just my bad eyes getting in the way. Once I realized this is the current, it made perfect sense.

So, I think this is a good point you brought up for Heidi to show an actual application of that circuit, and the result is very important and interesting.

Your example gives a good place for me to try and point out why proper analysis is important. A person might look at that circuit as say there are two time constants R1C1 and R2C2, and they should both equal to 40 microseconds in this example. Indeed, if I use a 50 ohm source resistance, one time constant comes out to be 40 microseconds. But, there is another at 0.3 nanoseconds that we can ignore practically.

But what happens if we have a mismatched case. Lets cut R1 in half from the value you gave in post #39. Now, the upper part has R1C1=20 us and the lower part has R2C2=40 us. Obviously this case is not compensated properly any more. However, now the slower time constant will be 33.33 us, and there will still be another fast time constant that we ignore. Note that the 33.33 us from proper analysis matches the what you expect from having R1 in parallel with R2 and C1 in parallel with C2. Both the fast and the slow time constant will reveal themselves in the response curve, but the fast one will be hard to see because it decays too fast. However, we could increase the value of Rs and eventually we would see both time constants in the response.

Ratch wants to ignore this fast time constant as say it's not there. He didn't say this directly, but he acknowledged that the circuit should have two time constants, and he insists that there are two equal time constants in the circuit. This is illogical and does not hold up to scrutiny when compared to proper analysis which shows a fast time constant in the response. I even put up the free response formula to show that T1 and T2 are both in the solution, but it is ignored as "over the head". I just feel the need to correct this because we're in a students thread, hence misinformation is a bad thing to allow without challenge. I agree that a lot of this is premature for the OP, but it's better to let it be known that what was said may have issues, even if the details are not fully comprehended. At least then the misinformation does not get carried further.

 

[Ratchit]

If there is a short in place of the voltage source, how can there be different initial voltages across the capacitors? In that case the two capacitors are connected in parallel.

You have asked the most interesting question thus far. The answer is that the caps will even out their voltages to one single voltage when the source voltage ceases. Let's look at an example circuit below. The time constant of each cap is 40 usec. You can easily see that the voltages across C1 will be 0.8 volts and C2 will be 0.2 volts while the source voltage is steady at 1 volt.. When the source voltage goes to zero, the voltage across both caps in parallel will be -0.8 + 0.2 = -0.6 volts at t=0, the instant the source voltage is turned off. Then it declines to zero exponentially. I know that is not intuitive, but Laplace does not lie. I hope I did not goof in setting up the node equation.

Ratch

 

[MrAl]

How about 200us? (5 "time-constants")

View attachment 81033

Hi Mike,

I like the practical example you brought up earlier too.

Using a ramped rise time is not much different than using a small series resistor Rs as we had been talking about. A ramp will not cause an infinite current but then i already mentioned that this was the case and we dont look at a DC source that way when it comes to these circuits unless we again apply practical constraints. And if we apply practical constraints then there's no question that there is more than one time constant. The difference between using a ramped rise and exponential rise is just that, Rs causes a fast exponential rise while a ramp of course causes a slower rise even without the resistor. We could also use a sine wave for that matter.

Also, i had already pointed out that when the resistors and capacitors are balanced so that both resistors and capacitors alone would produce a given voltage, the output will be a constant not a function of time. But those are isolated cases not the general case. For certain values we get a constant output so we can say that the response has no time constant, but we could still say that the two time constants are related in a specific way and to undo that upsets the balance and then we see again a different response other than constant, and we would have known this from knowing the time constants.

Here's my rendition of a state space representation of the circuit with added Rs perhaps small:
x1=(E-X1-X2)/RsC1-X1/R1C1
x2=(E-X1-X2)/RsC2-X2/R2C2
Vout=vC2=X2

Here we clearly see four time constants (in the denominators). So we can talk about the slope at a given point in the response based on knowing two time constants for each capacitor voltage. If we didnt know the time constants we could not figure this out, or at least when we do figure it out we end up with the time constants like it or not

BTW looking at an output response can not tell you all the time constants present in the circuit. It might help, but there could be hidden time constants that combine.

We might also note here that the original problem called for finding an "equivalent" time constant, as in a sort of total time constant. We can find that or find individual time constants. As long as we have at least one capacitor and one resistor we can find a time constant, and if we have a second resistor then we can find a second time constant. The second one may or may not do us any good.

 

[steveB]

MrAl,

This issue of the number of time constants is really confusing. Now you are saying there are 4 time constants, and saying there could be hidden ones is a possibility. This is just confusing for no reason. Time constants should not be able to hide. If one identifies all state variables, which is necessary to make a state space system, then all time constants will be seen in these state variables. Then, any other system variable will be a function of these states, so the same time constants will be there too.

When we look at your state space equation, we don't just look at the terms to find the time constant. You have to determine the A matrix and then find the eigenvalues for the A matrix. If the A matrix is diagonal, then you will see the time constants directly, but if not, you have to do it out formally, and often it is too hard to do this algebraically. In this example, the A matrix is not diagonal. Above, I already showed the A matrix and I found the algebraic formula for the time constants when R1=R2=R and C1=C2=C. Then for MikeMl's example I did it numerically for the case where the resistors and caps are not equal. (I actually also worked out the eigenvalues algebraically for the general case, but it is a messy equation that's too hard to use and show here.)

If anyone would actually pay attention to what I wrote, they would see the values do not correspond to the values in the denominators. It is not a simple RsC1, RsC2, R1C1 and R2C2, but there is a slow time constant formed by the parallel combinations of the resistors and capacitors (actually it's more complicated than that, but if Rs is small, accurate enough), and then there is a very fast time constant that depends on Rs, R1, R2, C1, C2, and goes to zero as Rs goes to zero. The A matrix is 2X2, so there are only 2 eigenvalues which reveals the 2 time constants.

This is all the standard approach used in formal analysis. I suppose one is free to define any RC from any random R and C in a circuit, and call it a time constant. People are free to define anything they find interesting. In MikeMl's application, the values R1C1 and R2C2 are certainly interesting to look at because you need to match them for a compensation function. However, the more useful definition of a time constant is "the value seen in the exponential decays of the system variables". (i.e. the T in exp(-t/T)

 

[MrAl]

Hi there Steve,

Well your argument has boiled down to what is "more useful". And that's certainly something we have to consider, but i think the scope of consideration is too small if we limit the definition to that which gives us certain solutions to certain specific problems. In this particular case where the paper is asking for a single time constant for example they want to limit us to a SINGLE one, while you yourself would be more comfortable with TWO. I believe you feel better with two because you can clearly see that one of the responses is dependent on two, not one or three or four. One of the types of responses is definitely dependent on two so it makes sense to think of these two. The two are actually easy to find if we just assume some values for the components, and we quickly see that the two constants that appear in the two exponentials are not the same for the general case.

I myself on the other hand, do not feel comfortable unless i am allowed to consider every element that can be combined into units of constant time to be a time constant. This is because i see usefulness in this view as well, and after all the units tell us they could have some relevance.
In the state equations i had shown previously i also stated that we can quickly find the slope of either voltage knowing some combinations of R and C that when multiplied come out to units of constant time. So in other words, we can find for example the slope of the voltage across C2 knowing the input step value E, the present voltage across C2, and the present voltage across C1, and also two multiplied values of R and C where the two products will be in general different from each other. Yet these values may have nothing to do with the time constants that actually determine the voltage response itself across C2 *in the analytical* solution. So that's why i see significance in thinking about other time constants too. If it were not for those two then we could not do this.
With a little thought we can even come up with the actual voltage across C2 over time without knowing anything else when we solve it numerically. During that process we would absolutely have to multiply three R's by two different values of C forming four different products of R and C. These products come out in units of constant time as constant Ohms times constant Farads equals constant Time. The units of x1 and x2 (lower case) come out to units of volts/second which is volts/time and that time is constant because all the R's and C's are constant. We would actually get the response knowing these four obscure time constants, and piecewise they actually make even more sense.

So it seems to me that you are not comfortable calling these products time constants maybe because you dont use them very often in this form, but im not sure what else to tell you. All things considered though i believe the time constants you found are time constants as well, but they have a different nature and different application that's all.

So your set is limited to only two while my set includes those two plus more
Dont get me wrong here though, i would not dare to apply them all in the same way.

This reminds me of the debate over what is a resonance and what is not. Some wish to restrict that definition to physical resonance alone while others have a more relaxed view.