LTSpice follows the conventions established by Berkley Spice, PSpice, and other Spices... The manual page you linked is for PSpice.
Spice's choice of current direction thru a source enables Spice to show power delivered by the source as negative power, while dissipative circuit elements show power consumed as positive power. This was already discussed by Ghar in this linked thread: https://forum.allaboutcircuits.com/t...nt-always-measured-negative-in-ltspice.40854/
I covered flipping resistors end-for-end (so that the sign of the current through the resistor is reversed) in post #3 of this linked thread:
https://www.electro-tech-online.com/threads/ltspice-current-probe.109196/.
Here is a simple sim that demonstrates Spice's power convention.
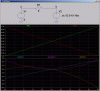
V1 is fixed at 5V, while V2 varies from 0V to 10V in small steps. The x-axis is V(V2) = V(b). The upper plot pane shows the current through V1 and V2 (per Spices's definition as discussed in the linked pdf). The traces were added to the upper plot pane by using the "amprobe" cursor and clicking on the voltage sources; the plotting is done automatically. Note that for different values of V2's voltage, at times the current in both sources and the resistor reverses...
The lower plot shows LTSpice's view of the power contributed by or dissipated by both sources and the resistor. The plots were obtained automatically by clicking on V1, V2 and R1 with the "thermometer" (power) cursor displayed. LTSpice shows if a source is contributing power or dissipating power seamlessly. Positive power is always dissipation. Note that the resistor only dissipates power. Note that all power goes to zero when V(V2)=V(V1). Note that when V(V2)=10, the power dissipated by both the resistor and V1 is 5W each.
How would you have done it? (Hindsight is always 20:20 )
)
Spice's choice of current direction thru a source enables Spice to show power delivered by the source as negative power, while dissipative circuit elements show power consumed as positive power. This was already discussed by Ghar in this linked thread: https://forum.allaboutcircuits.com/t...nt-always-measured-negative-in-ltspice.40854/
I covered flipping resistors end-for-end (so that the sign of the current through the resistor is reversed) in post #3 of this linked thread:
https://www.electro-tech-online.com/threads/ltspice-current-probe.109196/.
Here is a simple sim that demonstrates Spice's power convention.

V1 is fixed at 5V, while V2 varies from 0V to 10V in small steps. The x-axis is V(V2) = V(b). The upper plot pane shows the current through V1 and V2 (per Spices's definition as discussed in the linked pdf). The traces were added to the upper plot pane by using the "amprobe" cursor and clicking on the voltage sources; the plotting is done automatically. Note that for different values of V2's voltage, at times the current in both sources and the resistor reverses...
The lower plot shows LTSpice's view of the power contributed by or dissipated by both sources and the resistor. The plots were obtained automatically by clicking on V1, V2 and R1 with the "thermometer" (power) cursor displayed. LTSpice shows if a source is contributing power or dissipating power seamlessly. Positive power is always dissipation. Note that the resistor only dissipates power. Note that all power goes to zero when V(V2)=V(V1). Note that when V(V2)=10, the power dissipated by both the resistor and V1 is 5W each.
How would you have done it? (Hindsight is always 20:20
Last edited:

