How does the feedback work in an inverting op amp amplifier?

[MrAl]

Hello again,

Very good Heidi

It is good that you thought to use the DC analysis instead of transient.
Also, i realized we could have used the DC sweep analysis

I dont use LT Spice as much as others here i think, but i still like to use it from time to time. It works pretty good for free program. Thanks go out to Linear Tech for giving us this tool.

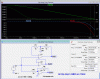
As a final note, we can see how the gain affects the voltage at Vn by sweeping from 1k to 50k. That shows us how the change levels off as the gain reaches roughly that upper limit of 50k. After that an increase in gain doesnt buy us too much more. Later when the transient response is done it will matter more though where the gain cuts back with frequency. At that time we'll want as much DC gain as we can get.

 

[Heidi]

Later when the transient response is done it will matter more though where the gain cuts back with frequency. At that time we'll want as much DC gain as we can get.

How lucky I am to have all you experts here along with my study. Thank you!

 

[MrAl]

Hi,

I am surprised we did not see a little more cut at 100kHz than that. Perhaps try a transient response next, at 1k, 10k, 100k, 1000kHz, or just try a constant AC source at those frequencies.

 

[Heidi]

As a final note, we can see how the gain affects the voltage at Vn by sweeping from 1k to 50k. That shows us how the change levels off as the gain reaches roughly that upper limit of 50k. After that an increase in gain doesnt buy us too much more.

Later when the transient response is done it will matter more though where the gain cuts back with frequency. At that time we'll want as much DC gain as we can get.

Did you mean the open loop gain of an op amp in the inverting closed-loop configuration will reduce with frequency, or the voltage gain will reduce with frequency? I got a little confused.

 

[Heidi]

Hi,

I am surprised we did not see a little more cut at 100kHz than that. Perhaps try a transient response next, at 1k, 10k, 100k, 1000kHz, or just try a constant AC source at those frequencies.

Here is how the voltage gain varies with frequency when the open loop gain of the op amp is 1k, 100k respectively.

Or, it's how the open loop gain of the op amp reduce with frequency when the open loop gain is 10k, 100k respectively, now the frequency is between 1Hz and 1000kHz.
Are these what you wanted me to observe?

 

[MrAl]

Hi again,

Ok sorry maybe i did not explain what i meant well enough.

Referring back to post #82, we see close to 9.542db at 1kHz and we see 9.535 at 100kHz. That is a change of less that 0.1 percent (less than one tenth of one percent) which is very small, and would be imperceptible in most applications, yet we are working with an op amp with a GBW product of only 1MHz. So something looks fishy (fishy in English in this context means something doesnt look right).

When i do an AC analysis i see close to 9.54db at 1kHz, and at 100kHz i see about 8.94db, which is roughly about a 7 percent change.
When i do an analytical calculation i get 9.542db and 8.898db for 1kHz and 100kHz respectively. That is roughly about a 7 percent change too.
Note: for the analytical approach the amplitude comes out to:
(3000*Aol)/sqrt(1.6e-5*Aol^2*f^2+(1000*Aol+4000)^2)
with R values 1k and 3k, and GBW=1e6 and i set Aol=1e6 also.

I have to wonder what is different between post #82 and these analyses.
Is your GBW set equal to 1e6 also? I have a feeling your GBW is set to 10e6 instead of 1e6.

 

[moty22]

Real op amp doesn't exist, op amp is a mathematical device that defined as: infinite gain, infinite input resistance,zero output resistance... It means that you can't explain op amp operation by a real op amp.
You are left with only Ohm's Law explanation as was offered by audioguru.
Have fun anyway.

 

[MrAl]

Hi,

Actually if you read post #86 you'll see that we are dealing with an imperfect op amp already but the imperfections may not be set right yet, or different than we originally intended

 

[moty22]

Hi MrAl, it seems that my phase lag is a few days, sorry to interupt.

 

[Heidi]

I have to wonder what is different between post #82 and these analyses.
Is your GBW set equal to 1e6 also? I have a feeling your GBW is set to 10e6 instead of 1e6.

Hi MrAl, you're right, the op amp's GBW in post #82 was set to 10Meg.

It took some time for me to learn what the gain-bandwidth product (GBW) for an op amp is (it was called unity-gain bandwidth in my textbook), and how it affects the voltage transfer function.

When i do an AC analysis i see close to 9.54db at 1kHz, and at 100kHz i see about 8.94db, which is roughly about a 7 percent change.
When i do an analytical calculation i get 9.542db and 8.898db for 1kHz and 100kHz respectively. That is roughly about a 7 percent change too.
Note: for the analytical approach the amplitude comes out to:
(3000*Aol)/sqrt(1.6e-5*Aol^2*f^2+(1000*Aol+4000)^2)
with R values 1k and 3k, and GBW=1e6 and i set Aol=1e6 also.

I reset the GBW to 1Meg and did both the simulation and hand calculation, both results agree with yours.

Vout(s)/Vi(s) = (-R2/R1) / [1 + s(1+R2/R1)/2*pi*ft] , where ft denotes the unity-gain bandwidth

With R1=1k, R2=3k, ft=GBW=10^6Hz, f=100kHz, Vi(jw)=1, the magnitude of Vout=2.78543=8.8978dB

(fishy in English in this context means something doesnt look right).

You're so thoughtful, thank you!

 

[MrAl]

Hi again,

Well you said you have some problems with the language so i thought i would clarify that
I am happy that we both get the same results now.

It is interesting that you bring up the gain bandwidth product and the unity gain bandwidth.

In some contexts these would be taken to be both the same. but i think if we want to be a little more strict in our definitions we might see a difference. This is because 'bandwidth' itself is usually defined as being the frequency that causes the response to drop down 3db from the normal gain, while "unity gain" means a gain of 1.
So in some contexts, we might see the Gain Bandwidth being defined as the -3db point, and unity gain being defined as the 0db point. There is some difference because the GBW will be greater than the unity gain bandwidth.

For the model we are using, the GBW probably refers to the -3db point, and you can check this by running the simulation at 1MHz. If the gain is 0db at that frequency then they are using the unity gain, but if the gain is -3db then they are using the stricter GBW definition. Because they actually call it GBW it's probably the -3db point they are setting, not the unity gain point. The unity gain point would then be something like 707kHz while the -3db point would be the full 1MHz. You could easily check this. The more accurate -3db point is actually closer to -3.0103db just for reference. It may still be approximate in the model though, so you could look for something close to that number.

 

[crutschow]

......................
It is interesting that you bring up the gain bandwidth product and the unity gain bandwidth.

In some contexts these would be taken to be both the same. but i think if we want to be a little more strict in our definitions we might see a difference. This is because 'bandwidth' itself is usually defined as being the frequency that causes the response to drop down 3db from the normal gain, while "unity gain" means a gain of 1.
So in some contexts, we might see the Gain Bandwidth being defined as the -3db point, and unity gain being defined as the 0db point. There is some difference because the GBW will be greater than the unity gain bandwidth.

For the model we are using, the GBW probably refers to the -3db point, and you can check this by running the simulation at 1MHz. If the gain is 0db at that frequency then they are using the unity gain, but if the gain is -3db then they are using the stricter GBW definition. Because they actually call it GBW it's probably the -3db point they are setting, not the unity gain point. The unity gain point would then be something like 707kHz while the -3db point would be the full 1MHz. You could easily check this. The more accurate -3db point is actually closer to -3.0103db just for reference. It may still be approximate in the model though, so you could look for something close to that number.

Just for grins I did simulations of the ideal op amp with a GBW of 1MHz for a follower configuration and and open loop configuration (with DC feedback to avoid saturation).
The follower had a gain of -3dB at 1MHz as was expected.
The interesting thing is that the open loop gain was 0dB (1) at 1MHz.
So the unity gain point refers to the open loop response, not the closed-loop response. (The feedback in the closed-loop configuration reduces the bandwidth).

Also, note that the inverting gain of 1 configuration has an equivalent non-inverting gain (the bandwidth gain) of 2 which means the closed-loop -3dB point is 500kHz, not 1MHz.

 

[Heidi]

Just for grins I did simulations of the ideal op amp with a GBW of 1MHz for a follower configuration and and open loop configuration (with DC feedback to avoid saturation).
The follower had a gain of -3dB at 1MHz as was expected.
The interesting thing is that the open loop gain was 0dB (1) at 1MHz.
So the unity gain point refers to the open loop response, not the closed-loop response. (The feedback in the closed-loop configuration reduces the bandwidth).

Also, note that the inverting gain of 1 configuration has an equivalent non-inverting gain (the bandwidth gain) of 2 which means the closed-loop -3dB point is 500kHz, not 1MHz.

Hi crutschow,

Could you please show me your schematics for a follower configuration and an open loop configuration with DC feedback?

I guess you use LTspice also, what's the name of the ideal op amp you used in LTspice?

What circuit can we use to detect the open-loop gain of an op amp? Could you explain why it works to me shortly please? (EDIT: briefly, not shortly)

 

[Heidi]

Before I get to know how to decide the frequency dependance of an op amp's gain by simulation program, let me say something I've learned recently about the open-loop gain of an operational amplifier.

I haven't study the internal circuits of an op amp yet, but if the open-loop gain Aol of an op amp can be described by an expression which is the same as that of a low-pass RC filter:

Aol(s) = A / (1+s/wb) -------- (1)

where 'A' is the op amp's dc gain and 'wb' is its 3-dB frequency.

For frequency w >> wb, the magnitude of Aol can be approximated by

| Aol(jw) | ≈ A*wb / w = wt/w ---- (2)

in which wt=(A*wb) is known as the unity-gain bandwidth of the op amp, and (2) can also be written as

Aol*w ≈ A*wb = wt
or
Aol*f ≈ A*fb = ft =GBW ---- (3)

which says that the product of an op amp's gain and the frequency at which the gain is measured is a constant equal to the op amp's unity-gain bandwidth for frequencies that are much larger than the op amp's 3-dB frequency. The product happens to be the definition of the gain bandwidth product (GBW). Therefore, if an op amp's open-loop gain can be described by (1), then for any frequency that is much larger than the op amp's break frequency, the op amp's GBW is equal to its unity-gain frequency.

As a test, let's see how an inverting opeational amplifier's gain relates to frequency and its GBW.

Assuming a finite open-loop op amp gain Aol, the closed-loop gain of the inverting amplifier is

Vout/Vi = (-R2/R1) / [1 + (1+R2/R1)/Aol] ----- (4)

inserting (1) for Aol into (4)

Vout/Vi = (-R2/R1) / [ 1+ (1+R2/R1)/A + (1+R2/R1)*s/A*wb ]
≈ (-R2/R1) / [ 1 + (1+R2/R1)*s/A*wb ], for A >> (1+R2/R1), A = dc gain of the op amp

Replacing s by ( jw)=(j*2*π*f) and wb by (wt/A)=(2*π*ft/A),

Vout/Vi = (-R2/R1) / [1 + (1+R2/R1)*(jf/ft)
= (-R2/R1) / [1+ (1+R2/R1)*(jf/GBW)

With R1=1k, R2=3k, GBW=1megHz, f=1meg

|Vout/Vi| = 3/√17 = -2.762 dB

 

[crutschow]

Below is my LTspice simulation of a 1MHz gain-bandwidth idealized op amp (opamp in the Opamps library modified for a 1MHz GBW).

The top is the open loop simulation.
DC feedback is provided by R1 and R2, with C1 suppressing the AC feedback down to a very low frequency.
Note that the gain is essentially 1 (0dB) at 1MHz with -3dB ocurring at 1.414MHz.

The middle is a unity-gain follower with a -3db bandwidth of 1MHz.

The -3dB bandwidth for the bottom unity-gain inverter is 500kHz.

All as theory would predict.

 

[Heidi]

Thanks and sorry, crutschow, I think I made a terrible mistake in English in post #93, "Could you explain why it works to me shortly please?", actually I meant "could you explain why it works to me briefly please". Please forgive my poor English.

I need some time to consider the top two circuits, if I still can't realize how they work and what their purposes are, I'll come back and ask for your help again.

 

[Heidi]

Can someone give me a hint about why the output voltage is less than the input in the right circuit? Where should I start to analyze it? The input is a sine wave with a magnitude of 1 volt and frequency 100Hz.

 

[Heidi]

Is the circuit on the left not an equivalent model of the one on the right? Why?

 

[JoeJester]

Heidi,

You might find this four part series interesting .... https://masteringelectronicsdesign.com/buildi-an-op-amp-spice-model-from-its-datasheet/

Are you using 100 farad capacitors?

 

[Heidi]

Heidi,

You might find this four part series interesting .... https://masteringelectronicsdesign.com/buildi-an-op-amp-spice-model-from-its-datasheet/

Are you using 100 farad capacitors?

Thank you JoeJester.

Yes, 100 farad. Perhaps you know the 100F cap has a special function in crutschow's top circuit in post #95? I was trying to figure out how that circuit is operating.